在混合仿真中，必然存在机电暂态和电磁暂态两侧数据的交互。为了分析问题的方便，假定机电暂态侧用戴维南等值电路代替，并向电磁暂态侧传送瞬时电压V&c (t) ；电磁暂态侧用诺顿等值电路代替，并向机电暂态侧传送基波电流I&e (t)；机电暂态计算步长为DT ,电磁暂态计算步长为Dt ；电磁暂态侧仿真程序为TE(transient electroMagnetic)，机电暂态侧仿真程序为TS(transient stability)。下面对几种数据交互方式进行讨论。

    5.2 机电侧延时一个机电暂态仿真步长的数据交互方式

    这种数据交互方式的过程如图3 所示，具体实现步骤如下：

    （1）TS 在t时刻传递电压V&c (t)给TE 程序，更新机电暂态侧的等值电压源。

    （2）TE 在[t,t + DT ]时间段内以步长Dt 计算N 次，直到t +DT 时刻。

    （3）在t +DT 时刻，根据前一个周期的电流瞬时值提取出基波电流有效值( ) e It +DT 并传递给TS，更新诺顿电路中的等值电流源。

    （4）TS在[t,t + DT ]时间段内以步长DT 计算，得到新的接口电压( ) c V& t + DT ，继续在下一个机电暂态仿真步长时间点上进行数据交互。如果没有故障或者操作发生，重复前面的计算过程。

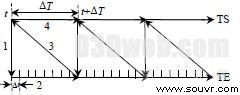
图3 TS和TE串行数据交互方式

    上述数据交互方式是一个典型的串行计算过程，实质是先根据机电侧t -DT 时刻的等值参数信息在区间[t -DT,t]上进行电磁侧的求解，在此过程中机电侧程序处于等待状态；然后根据t时刻的电磁侧等值参数信息进行t时刻机电侧的求解，在此过程中电磁侧一直处于等待状态。目前已有的混合仿真接口数据交互算法大都采用这种方式。

    5.3 两侧并行的数据交互方式

    这种数据交互方式如图4 所示，具体实现步骤如下：

    （1）TE 在t时刻传递接口参数到TS程序，更新诺顿等值电路，TS 在t时刻传递接口参数给TS程序，更新戴维南等值电路，在[t,t + DT ]时间段内保持诺顿和戴维南等值电路参数不变。

    （2）TS在[t,t + DT ]时间段内以步长DT 计算到t +DT 时刻，得到新的接口变量参数，同时TE以步长Dt 计算N 次后直到t +DT 时刻，得到新的接口变量。若没有故障或操作发生，重复前面的计算过程。

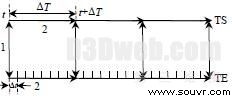
图4 TS和TE并行数据交互方式

    从上述交互过程可以看出，机电和电磁暂态侧在仿真过程中都不需要等待，两侧各自并行计算，因而提高了仿真速度，满足了在接口处实时交换数据的要求，但是每一侧在t +DT 时刻采用的都是对侧t时刻的等值信息，因而存在一定的交接误差，影响了计算精度。

    5.4 两侧相互迭代的数据交互方式

    这种数据交互方式如图5 所示，具体实现步骤如下：

    （1）TS 在t T +D 时刻传递电压( ) c V& t + DT 给TE，更新机电暂态侧的等值电压源，同时TE 传递电流有效值( ) e It + DT 给TS。

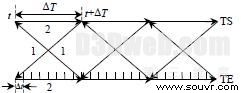
图5 TS和TE相互迭代的数据交互方式

    （2）TE 在[t,t + DT ]时间段内以步长Dt 计算N 次后直到t +DT 时刻，同时TS 也从t时刻计算到t +DT 时刻。步骤（1）、（2）都完成后，若没有故障或者操作发生，在下一机电暂态仿真步长点重复前面的计算过程。

    实际上步骤（1）和（2）是交替在一起进行的，其中包含了复杂的非线性迭代和收敛运算。这种数据交互方式虽然在精度上有很大的提高，但是计算量过于庞大，计算效率低下，实用性差。

    6 数据形式的转换和基波相量的提取

    对于机电侧而言，它提供的等值参数是基于三序相量的戴维南电路形式，而在电磁侧程序中，网络中的元件差分离散化后会得到一系列并联的等值电阻和等值电流源形式，构成了暂态计算等值电路，然后再通过差分后的节点导纳矩阵进行网络求解，因而有必要先把戴维南等值电路转化为诺顿等值电路形式，然后把基于正、负、零序的诺顿等值导纳和等值电流源转换成基于a,b,c 三相的瞬时值模式，最后并入到电磁侧网络方程中求解。

    类似地，对于电磁侧而言，它提供的是基于三相瞬时值模式的诺顿等值电路形式，因而有必要先把这些离散的瞬时值转换成基于相量的基波有效值形式，然后通过线性变换把a,b,c三相空间的数据转化为正、负、零序相空间的数据，最后并入到机电侧网络方程中求解。

    电磁侧基波相量的提取大都基于傅里叶变换，该算法能够保证基波数据提取的准确性，即使在接口处波形和电流畸变比较严重的情况下，仍然可以使用傅立叶变换得到整个频谱的信息，但是计算量过于庞大。

    曲线拟合算法(curve fitting algorithm，CFA)是一种基于最小二乘的分析方法，它不用考虑其它高次谐波和直流分量，可以快速准确地提取出对应的基波相量[7]。另外，基于傅里叶变换的算法在提取基波相量时需要一个周波的序列数据，而CFA 方法不受此限制，因而在使用上具有更大的灵活性。

    7 电磁侧与实际物理装置相连的意义

    实时性一直是电力系统数字仿真追求的目标之一，机电暂态和电磁暂态数字混合仿真也不例外。但具有更大意义的是，不仅机电暂态侧和电磁暂态侧能够满足实时交互的要求，而且在电磁暂态侧可以与实际的物理装置连接并实时交互。

 &