2 数字混合仿真方法的基本概念

    2.1 数字混合仿真方法的分类

    一种数字混合仿真方法是在暂态过程开始后一段较短的时间内对全系统作电磁暂态仿真，等到电磁暂态过程大为减弱或基本结束时再转为对全系统的机电暂态仿真。这种方法基本上反映了系统的动态变化过程，它根据时间先后采取不同的仿真方法，可以定义为基于时间的混合仿真方法。

    另外一种数字混合仿真方法是对整个网络进行分块，具有快速暂态过程的部分采用较小的步长进行电磁暂态仿真，常规交流系统采用较大的步长进行机电暂态仿真。这种根据系统各部分空间位置的不同以及暂态过程的快慢采用不同仿真技术的仿真方法可以定义为基于空间的混合仿真方法。本文主要研究的是基于空间的混合仿真方法。

    2.2 数字混合仿真功能的实现
   
    一种实现思路是在一个软件包中开发出具有混合仿真功能的集成模块，类似于NETOMAC软件的处理方法，机电和电磁暂态仿真都在同一个程序中实现。但两者在实现方法上差异很大，难以集成在一起，现在已经很少采用这种方法了。

    另外一种实现思路是利用已有成熟的机电和电磁暂态程序，选择合适的接口交互算法来实现混合仿真功能[17]。通常以机电(或者电磁)暂态程序为主程序，另外一个程序通过用户定义接口作为子程序嵌入其中。在一些新的实现方案中，两侧程序不再有主次之分[9]，都作为独立的程序参与混合仿真计算，明显提高了混合仿真的灵活性和效率。

    2.3 数字混合仿真方法的基本原理

    机电暂态和电磁暂态数字混合仿真的基本原理如图1所示，系统中的常规交流部分动态响应过程相对较慢，可以采用机电暂态程序进行仿真，数据中只包含基波相量，步长假定为10 ms；而含有HVDC/FACTS 装置的部分具有快速的动态响应过程，采用精确的电磁暂态程序进行仿真，数据基于瞬时值模式，步长假定为50ms。

图1 机电暂态和电磁暂态混合仿真的原理

    在一侧进行仿真时，另一侧采用合适的等值电路来代替，数据交换时刻只发生在机电暂态步长点，即每隔一个机电暂态仿真步长两侧才交换一次数据。在上述假定的仿真步长下，机电侧进行一步计算，电磁侧需进行200 步计算，在这一个机电暂态仿真步长的仿真过程中，两侧没有数据交换。

    由于机电暂态和电磁暂态过程在仿真机理、数学模型、数据表示方法等方面有着很大的不同，因而混合仿真中机电侧基于正、负、零序网络的基波相量和电磁侧基于a,b,c 三相的瞬时值之间必须进行数据形式的转换，而且在电磁侧得到的离散序列数值也要转化成基波相量传递给机电侧，下文将对该问题作进一步探讨。

    3 接口位置的选择

    含有HVDC和FACTS装置的电力系统，其接口位置一般都选在HVDC 换流器交流侧母线或FACTS装置连接变压器一次侧母线处，这主要是基于以下几点考虑：

    （1）缩小了电磁暂态仿真的范围，减轻了电磁暂态仿真程序的计算负担，接口的数量较少。

    （2）换流器母线处的设备如滤波器、静止无功补偿器(static var compensator，SVC)装置等都被包含在电磁暂态仿真程序中，可以更好地分析它们的有关特性。

    （3）母线处的电流或者电压数值相对比较稳定，有利于保证数值计算的稳定性。

    有些学者还提出了另外一种思路[5-6]，即在交直流混合仿真中把接口位置从换流器母线处延伸到交流系统内部，如图2 所示。在弱联系的交流系统中，接口位置如果扩展到交流系统内部，则接口处的电压和电流的畸变程度将大为降低，同时接口的选择更加灵活，根据分析问题的需要可以在交流系统内部的不同位置任意选择接口。但是这种方案导致电磁暂态仿真程序的计算量大为增加，接口处理更加复杂，明显降低了混合仿真方法的计算效率，因而较少使用。

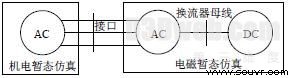
图2 延伸到交流系统内部的接口位置

    4 两侧的等值电路形式

    4.1 机电暂态侧等值电路形式

    在电力系统混合仿真中，计算某一侧网络时，对侧都用合适的等值电路来代替。由于机电暂态侧网络的仿真规模比较庞大，并且通常含有有源系统，而且网络中的参数可以认为近似符合线性关系，所以相对外部系统来说，可以直接用戴维南或诺顿等值电路来代替[18]。

    值得注意的是，在交直流混合仿真中，机电暂态侧的基波等值阻抗不能真实反映系统的谐波阻抗特性，存在难以描述系统的高频特性等问题[9]，若采用与频率相关的等值阻抗形式来反映机电侧的网络特性，则在一定程度上可以弥补基波阻抗形式的不足。

    4.2 电磁暂态侧等值电路形式

    由于电磁侧元件和结构较复杂，可能包含HVDC、FACTS或其它非线性电力电子元件，甚至只含当电磁侧是常规交流网络时，可采用类似机电侧的诺顿等值电路形式；当电磁侧是FACTS 类型元件时，根据该侧元件的特性，一般可采用恒功率负荷、恒阻抗或者恒电流源等类似形式[21-22]；当电磁侧含有HVDC系统时，可采用电流源并联一个恒定大电阻的近似诺顿等值电路的形式。

    4.3 等值电路形式的评价

    上文提到的无论是机电侧还是电磁侧的等值电路形式，本质上都是一种静态等值，因而不可避免地存在非线性误差和固有的局限性。从理论上说，动态等值具有更好的精度，但是动态等值技术本身还有很多需要完善的地方，另外对于混合仿真来说，采用动态仿真等值计算量太大，过程也很复杂，难以应用到混合仿真中，目前在混合仿真中诺顿等值电路或者其它的类似形式是一种比较实用和有效的方法，如果能够根据不同的网络结构和特点制定出合适的等值电路和正确求出对应的等值参数，也能满足工程计算的精度要求。

    5 主要数据交互方式