生物具有的力学特征如: 应力- 应变关系的非线性、滞后回线的存在、应力松弛、蠕变等等, 实质上是同一物理现象, 即都是生物体材料的粘弹性的表现。因此可以预料, 它们必然有统一性, 可以期望用某种理论和统一的数学关系来表达。要建立一个虚拟手术中基于真实切割数据的软组织力觉模型, 需要解决的两个重要问题是: 确定软组织变形过程中应力- 应变之间的关系, 这与材料的杨氏模量有关; 确定软组织的平均断裂强度。

    4.1 生物材料断裂强度

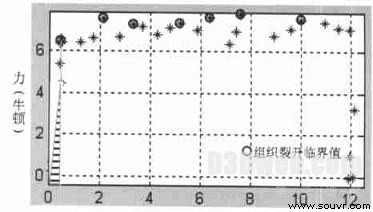
    要确定生物材料的断裂强度Jc [1 ] , 不像确定刚性材料的断裂强度那么容易, 因为生物材料断裂韧度, 像它的其它性质如弹性模量一样, 会随温度、环境、老化程度、方向等的变化而变化。经过多次试验观察发现, 在组织不同位置, 断裂强度Jc值不相同, 没有变化规律可寻, 如图7 所示, 但断裂强度有Jc 一个变化范围。

刀刃位置(厘米)

图7 　切割力相对于刀刃位置典线

    由于计算机采集到的数据都是离散的, 用采集到的手术刀上的作用力和切割位移来计算手术刀在切割过程中所做的功, 如下式所示:

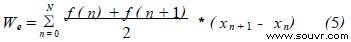
    式中f ( n) 和x n 分别n 3 T 为时刻采集到的刀刃上的作用力, 以及刀刃切割点所在的位置, T为采样周期。

    假设组织的平均断裂强度为Jc , 裂缝的面积是a ( s) , 则组织断裂消耗的能量为

    Ws = Jca ( s)                           (6)

    因为材料样本被切成厚度为1cm 的长条, 可以认为切割近似如图8 所示的那样, 手术刀刃切割点位移是从a →b →c →d :

    a) a →b 是力增加的过程, 此时只有粘弹性变形, 力没有达到断裂强度;

    b) 在b 点, 切割力达到断裂强度, 样本被切开裂缝;

    c) b →c 裂缝扩展过程;

    d) 到c 点, 手术刀停止切割, 样本弹性变形消失, 裂缝顶点恢复到d 点。

    abcd 包围的斜线阴影部分是样本裂开所需的手术刀做的不可恢复性的功; 横线阴影部分是手术刀做的可恢复性的功, 即是转化为样本材料弹性能量U 的功, 如图8 所示横线阴影部分。当手术刀离开时, 弹性能量消失。当切割的裂缝长度为l ,深度为x 时, 有下式

    Ws = Jcl x                   (7)

    储存在组织里的弹性能量U 并不是一个不变的值, 而是在切割过程变化的值, 因为切割工具非常锋利, 弹性变形不会太大, 所以弹性能量U 也不太大。假设组织裂开时, 采样点为C , 则储存在组织内最大的弹性能量U 为图8 所示的横线阴影部分, 可用下式计算

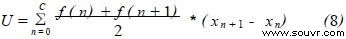
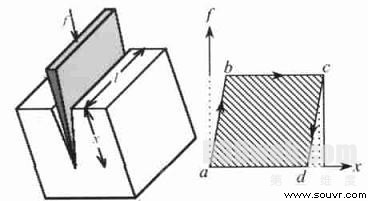
图8 　切割所作的功

    组织裂缝扩展所需的能量和储存在生物体组织内的粘弹性能量, 所以有

    Ws = Wc - U            (9)

    因此, 可得到一个断裂强度J c 平均值

    因此, 可得到一个断裂强度J c 平均值

    如图7 所示, 当切割时手术刀运动速度较快,速度为V = 2 m m/ s , 环境温度为22°, 皮肤组织的断裂强度Jc 变化范围为016 ～ 018kJ / ㎡ 。由式(10) 计算得到Jc 平均值为01687 kJ / ㎡ 。

    4.2 应力- 应变关系

    在本文研究中, 把切割过程分为两段来分析:

    第一段是切割工具与生物组织接触, 只有粘弹性变形, 生物组织没有被切割开; 第二段是生物组织被切开裂缝, 在切割工具的作用下, 裂缝扩展过程。这两段的分界点是切割力第一次达到组织的断裂强度, 瞬间裂开时刻。

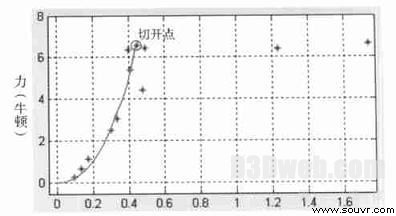
位置(厘米)

图9 　皮肤组织应为vs 变形典线

    由图9 分别是肝脏和皮肤组织在切割过程中的应力- 应变曲线。因为生物组织是粘弹性体, 所以应力应该是变形u 变化量和速度v 的函数。假设t 时刻, 变形为u1 , 速度为v1 , 则应力为F1

    F1 = g ( u1 , v1)      &nb