来源：第三维度
    作者：宋新立 汤涌 刘文焯 仲悟之 吴国旸 刘涛
    单位：中国电力科学研究院

    摘要：全过程动态仿真是将电力系统机电暂态和中长期动态过程有机地统一起来的一种数字仿真。仿真模型中的时间常数差别很大，是典型的刚性非线性系统。数值积分算法是全过程动态仿真的核心。分析非线性刚性系统求解的特点和电力系统动态仿真中现有数值积分算法存在的主要问题，提出一种新的适合全过程动态仿真的组合数值积分算法。该算法有机地结合了固定步长隐式梯形积分法和变步长吉尔(Gear)法的优点，克服现有变步长吉尔法在机电暂态过程中计算效率低下和间断处理复杂的问题。算例仿真与分析的结果表明了新算法的有效性和可行性。

    0 引言

    电力系统全过程动态仿真是将电力系统机电暂态、中期和长期过程有机地统一起来进行数字仿真，能够描述电力系统受到扰动之后整个连续的动态过程，是电力系统规划设计、调度运行和科学研究的重要仿真计算工具之一[1-3]。随着中国特高压骨干电网的快速建设和智能电网的加快实施，规模巨大的全国性交直流互联电力系统即将形成，这使得电力系统特性发生变化，系统的静态和动态行为变得更加复杂。因此，为建设中国统一坚强的智能电网，迫切需要研究和分析这种非线性超大规模电力系统动态特性机制、严重事故特征及其智能稳定控制策略的全过程动态稳定仿真技术。

    全过程动态仿真主要涉及发电机及其励磁系统和动力系统、动态负荷、电力电子元件等众多动态元件和输电网络等组成的非线性动态系统[4-5]。描述这一非线性动态系统的是一组高阶的微分方程组和代数方程组。全过程动态仿真采用时域仿真法计算电力系统动态元件及其控制系统的动态过程。仿真中模型的时间常数差异很大，混合着快速和慢速动态过程，是典型的刚性非线性动态系统。时域仿真计算就是采用适当的数值积分方法求解微分代数方程组的初值问题。因此，数值积分方法是整个全过程动态仿真技术的基础和核心。

    电力系统全过程动态仿真用于研究电力系统在受到干扰之后系统较长时间的机电过渡过程。仿真时间从几秒到数十分钟甚至若干个小时，时间跨度大。因此，需要采用自动变步长积分方法，在系

    统的快变阶段(机电暂态)使用小步长计算，而在慢变阶段(中长期动态)使用大步长。现有全过程动态仿真程序的数值积分方法大多采用吉尔类变步长方法，例如瑞典的SIMPOW程序[6]、法国和比利时的EUROSTAG程序[7-8]和中国电力科学研究院开发的全过程动态仿真程序[9]。这种方法的优点是暂态过程及中长期动态过程可以采用统一的模型和

    数值积分方法，在中长期动态过程中可以大步长进行仿真。但在应用实践中发现这种方法的主要缺点和问题为：1）机电暂态过程中计算步长过小，导致仿真效率很低，例如，对于中国东北—华北—华中联网系统的仿真计算，全过程动态仿真程序在快变的机电暂态阶段，其计算速度要比现有暂态稳定程序慢5~6倍；2）算法难以处理模型中的间断环节。

    本文分析刚性系统求解的特点和现有电力系统动态仿真中数值积分方法的主要问题，提出一种新的适于电力系统机电暂态及中长期动态过程的组合数值积分算法，并通过算例说明新算法的有效性和可行性。

    1 刚性系统求解的特点

    1.1 求解时的数值稳定性要求

    对于非线性系统：

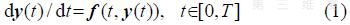
    式中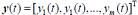：为待求的m维函数向量；t为时间；T为仿真总时间。如果是刚性系统，则雅可比(雅可比)矩阵∂fi/∂yi的特征值λi(i=1,2,.,m)的实部小于0，且实部绝对值的最大值和最小值差别很大..[10]。

    对于刚性系统的数值积分求解，为保证方法的数值稳定性，选取步长h很重要，需要使得每个步长值ih都落在所采用的数值积分方法的绝对稳定区域内，即满足。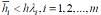

    当方法的绝对稳定区域有限时，例如，常见的2阶龙格–库塔法等显式方法，步长要限制在1/maxReiiλ的数量级，即系统最小时间常数的数量级。如果仿真时间T(即数值积分区间[0,T])与最大时间常数同级，则积分步数N=T/h就与刚性比同级，是一个很大的数。因此，要克服这种步长限制，要求数值方法的绝对稳定区域包含左半复平面，即要求方法具有A稳定性。而具有A稳定性的方法必是隐式的，且其最大阶数是2阶。梯形积分法是具有最小误差常数的A稳定方法[10]。

    1.2 求解时的收敛性要求

    由于具有A稳定的数值积分法是隐式的，因此，每积分1步必须伴随1个隐式方程的求解过程。非线性方程的求解通常有简单迭代法和牛顿迭代法2种。现以梯形积分法为例说明刚性系统中求解的特点[11]。式(1)的梯形求解公式为

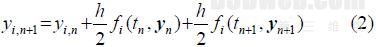
    式中n为计算步数。当使用简单迭代求解时，方 程(2)的收敛性条件为

    式中λ为相应的雅可比矩阵按模最大的特征值(电力系统全过程动态仿真中λ最大模值的数量级为10的2次方)。对于刚性系统来说，为满足收敛条件，h被限制在很小的范围内(电力系统全过程动态仿真中h的数量级为10的−2次方)，实际上这与显式方法的稳定域对h的限制是一样的，所以，简单迭代法不能满足数值积分中使用较大步长的要求，必须使用牛顿法迭代求解。

    牛顿法求解时，公式(2)改写为

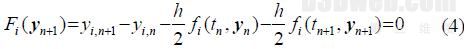
    则牛顿迭代可表示为

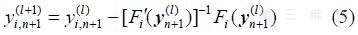
    式中：l 为是迭代次数；为 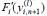关于变量y的雅可比矩阵，并在 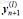取值。实际积分计算中雅可比矩阵的元素值经常是慢变化的，对于1步或步长不变的若干步，矩阵不必重新计算，仅在不收敛或误差较大时重新计算。该迭代方法称为拟牛顿法。迭代初值通过显式积分方法容易预测得到。

    由此可知，对于电力系统全过程动态仿真来说，若要使用较大的仿真步长，则不能使用简单迭代求解，而采用牛顿法联立求解是有效方法之一。

    2 现有数值积分算法的分析

    2.1 电力系统全过程动态仿真中微分代数方程的一般形式电力系统全过程动态仿真中需要求解的微分代数方程组可表示为

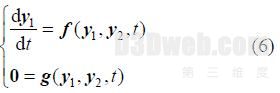
    式中：微分方程表示电力系统元件的动态特性，是系统的状态方程；代数方程表示电力系统元件的静态特性，主要是系统的网络方程；y1为n1个状态向量(微分变量)；y2为n2个代数向量(代数变量)。

    微分代数方程组的阶数为n1和n2之和。电力系统全过程动态仿真对象通常是大规模交直流电力系统，其规模可达成千上万个母线和支路、数千台发电机及其控制系统、数十条直流输电线路。因此，式(6)中的方程阶数常达数万阶以上。

    由于微分代数方程组(6)的代数约束方程的雅可比矩阵是非奇异的，所以电力系统全过程动态中的微分代数方程组的秩为1，是一个隐式的非线性微分方程组，能够使用刚性微分方程理论和算法进行数值积分求解[12]。

    2.2 基于吉尔法的变步长积分方法

    吉尔法是公认的求解刚性问题的有效方法之一，特别是对于计算精度要求不高的系统。对于变步长的吉尔积分法，其计算步骤主要包括预测、校正迭代、截断误差计算和自动变阶变步长控制4 步[13]。吉尔法能够自启动，起步时使用1阶。由于只有2阶及以下的吉尔法的稳定域能够覆盖复平面的左半平面，所以使用的最大阶数为2阶。校正迭代采用拟牛顿法，因而吉尔法满足刚性系统求解的数值稳定性和收敛性要求。

    电力系统微分代数方程组的特征值多为复数，时域解表现为振荡曲线。经典吉尔法应用到电力系统微分代数方程时，则会遇到绝对稳定域覆盖复平面的右半平面，导致在有的情况下出现计算危险性问题[8]，即仿真出的电力系统电气量或控制量的阻尼比实际结果要强，从而使仿真出现较大偏差，得出错误的结论。虽然选择高精度或小步长可避免这种问题，但代价是对于本来不存在计算危险性的系统，仿真速度也很慢。因此，电力系统全过程动态仿真中需要对其微分代数方程组的微分和代数变量分别处理，对微分变量使用隐式亚当姆斯(Adams)法(2阶隐式亚当姆斯法就是梯形积分法)；对代数变量使用吉尔法。这种方法的实现步骤与经典的吉尔法完全相同，所不同的是校正和截断误差计算中的系数需要根据变量的性质取不同的值[8]。

    2.3 吉尔法使用中的步长控制问题

    通过大量的电力系统动态仿真实践发现，对于吉尔法中迭代误差和变步长控制策略，很难找到一种合理的参数，使得在不同的电力系统运行方式和不同的故障形式下，对机电暂态和中长期动态过程都具有较满意的仿真步长。如果误差控制严格，机电暂态过程步长容易过小，例如，小于1 ms。虽然对于中长期动态过程，这种严格的误差控制能够使仿真采用合理的大步长，但在暂态阶段仿真速度很慢；反之，如果误差控制条件放宽，则虽然机电暂态的初期步长控制的比较合适，但在随后的机电暂态及慢变(中长期动态)过程中，累积误差会很大，校正迭代中往往不收敛，需要强制减小步长，计算量反而增加很多；此外，从编程实现方面考虑，仿真中自动更改控制参数实现较困难。所以，现有的吉尔算法很难找到一个误差和步长控制的计算方法，以使不同的仿真算例在快变和慢变过程都能使步长得到合理的控制。实践中，为保证计算可靠，常常采用误差控制严格的方法，以使得仿真精度有保证，但大大限制了仿真速度。

    电力系统全过程动态仿真中往往有频繁的自动装置动作，产生很多的机电暂态过程，导致在较长的仿真时间内积分计算只能使用很小的步长。

    2.4 吉尔法使用中的间断问题分析

    采用吉尔法时，当某个变量积分区间包含间断点时，在预测阶段不能预知右端函数会发生间断，即由一个函数变换为另一个函数，导致在校正阶段或截断误差计算中该变量的误差很大，因此，算法需要将步长缩小，同时雅可比矩阵也要重新计算，直到积分区间不包含间断为止。然后因误差减小，步长放大，又将间断点包含在积分步中间，因此又将缩小步长。这样反复多次，最后以小步长“爬”过间断点。对于小规模刚性系统的仿真，例如航天领域等，间断问题已有不少解决方法[13]。

    对于电力系统全过程动态仿真来说，控制系统中存在大量的限幅、死区等非线性环节[14-15]，例如，一台发电机的励磁系统和调速系统模型中，间断环节数量常超过10个，而对于一个具有千台以上发电机模型的大规模电力系统来说，这种环节的数量非常大。小步长引起的计算步数增加及反复的雅可比矩阵修改和重新分解都使计算量增加，计算效率低下。

    目前电力系统动态仿真中有2种解决这一问题的措施：

    1）先假定函数是连续的，正常积分，该步完成后，如果发现跨过间断点，则需要计算出断点出现的准确时间，并抛弃刚刚完成的积分步，然后把步长调整到断点处，以顺利通过断点，之后换为另一个函数。该方法在SIMPOW程序中被采用，其优点是间断计算准确，但缺点是对大规模电力系统来说，控制系统间断点数量非常多，反复回退到断点处，使得积分效率很低，而且编程实现时判断处理很复杂。

    2）迭代中遇到间断时，把发生间断的控制系统模块独立出来，单独实行小步长积分计算完成该积分区间步，同时修改该模块求解变量的截断误差计算公式，以使该模块变量不影响整个系统的误差判断。这种方法的主要问题在于单独模块的小步长积分方法及间断点过后的处理。如果采用不变阶的固定步长计算，则虽然编程实现简单，但是算法中变量的2阶导数不易计算出；如果采用变阶变步长算法，很难保证每次小步长后计算方法都是2阶。变量的2阶导数不能计算出来将导致该模块的后续积分计算误差增大，使得整个系统积分步长减小，因而存在与不处理间断导致步长小的类似问题。另外，该方法需要独立的模块积分计算，也存在编程实现复杂的问题。

    间断问题大多数出现在系统快变阶段，此时，变量变化剧烈，含限幅等非线性环节的微分方程的右端函数经常切换。在电力系统控制系统模型中，因含间断的环节数量众多，采用上述2种措施进行编程开发的难度很大，程序的可靠性难以保证。

    2.5 固定步长的隐式梯形积分法

    现有的电力系统暂态稳定仿真程序中固定步长的隐式梯形积分法已经比较成熟，得到了广泛的应用，例如国内电力系统常用的PSD-BPA电力系统分析程序和PSASP电力系统综合分析程序[16-17]。这种算法的优点是：1）具有A稳定性，能够自启动计算；2）机电暂态过程中积分步长通常为较小(0.01~ 0.02 s)，能够满足电力系统机电暂态过程仿真要求(最大仿真时间一般在20~30 s以内)；3）采用简单迭代法求解，控制系统的间断环节易处理。所以，该方法具有编程简单可靠、便于扩展的优点。算法的具体描述见文献[18]。

    但是这种适于机电暂态过程的积分方法不能直接推广应用到中长期动态仿真程序。原因是该方法采用简单迭代求解，由1.2节的迭代收敛性要求知，仿真步长较小，而中长期动态的慢速过程时间很长，长达数分钟甚至数十分钟，如果仿真步长一直很小，则仿真步数达数万步以上，仿真效率很低。

        上一页          下一页