来源：第三维度
    作者：王胜正 , 　杨　杰
    单位：上海交通大学

    摘要: 为了解决多投影仪拼接系统中的几何变形与图像融合问题,提出了一种新的自动非线性几何校正和图像边缘融合方法. 首先定义了屏幕空间与投影仪之间的几何关系和计算方法;然后用智能相机摄取屏幕上的激光点阵与标准网格投影图像,根据摄取的图像特征计算屏幕空间与投影仪之间的投影变换矩阵,由投影变换矩阵计算得到投影图像的双3 次几何变形曲面,从而可以反算得到曲面的控制点,实现对投影图像的非线性几何变形;最后给出图像边缘亮度融合算法. 实验结果表明,所提出的方法适用于多投影仪拼接的实时仿真系统。

    对大多数可视化系统需要利用多台投影仪拼接在一起,显示一个逻辑上一致的全景图像,这种解决方案有两个关键问题需要解决. 其一,透视投影图像投影在弧形幕或球幕上,图像会发生几何变形,因此必须对投影图像进行几何变形校正;其二,多个投影仪投影图像拼接在一起,图像之间要么有一个缝隙,要么有一条2 倍亮度的重叠区,这两种情况都会严重影响显示效果. 因此,必须把拼缝处的图像融合,使重叠部分的图像色彩尽可能一致.

    以往对图像几何校正与图像融合的解决方法是购买昂贵的投影仪或者图像融合机(如3D Percep2tion) ,对于前者,这些投影仪通常有内嵌光学融合镜头和几何校正芯片,后者即把多台投影仪输出的视频图像输入融合机,通过融合机的几何校正和融合后分别输出到投影仪,但这些方法不仅昂贵,而且维护相当困难,都必须手动调节,只有专业人员才能使用. 近年来,出现了很多自动几何校正与边缘融合方法. 例如:Raskar 等[124 ] 对投影仪的校正做了大量工作,并且成功地利用双照相机定位方法进行几何校正,但该方法需要对双相机进行校准,故对于小型系统比较适合,对于大型环幕,安装配置难度大;Ashdown 等[5 ] 研究了基于投影仪2相机的平面投影幕的自动几何校正方法;Okatani 等[6 ,7 ] 对基于投影仪2相机的自动校正方法做了很深入的研究,提出并证明了平面投影幕与相机以及平面投影幕与投影仪对应的透视几何关系;Baar 等[8 ] 利用二次曲面变换方法对投影图像进行几何变形;Song 等[ 9 ] 提出一系列非参数几何校正的理论方法;黄永锋等[10 ] 推导了2D 与3D 空间中变换的几何关系; Li 和Bourke等[11 ,12 ] 分别对光学边缘融合和软边缘融合进行了讨论与回顾.

    本文提出了一种自动非线性几何校正和边缘融合方法,通过对屏幕上的激光点阵与计算机输出的标准网格进行计算机视觉匹配,获得屏幕与投影仪之间的三维几何变换关系. 由该几何关系推算投影图像的双3 次曲面变形图像,实现非线性几何校正;并用边缘融合函数,对计算机帧缓存中的图像实现边缘亮度融合.

    1 　投影幕与投影图像的几何关系

    1. 1 　透视投影图像几何变形

　　在虚拟现实系统中,通常需要将3D 图像通过设备投影在物理屏幕上,目前,常见的屏幕有屏幕墙、环形柱幕、球幕、球带等形状. 当投影屏幕是弧形柱幕、球幕或球带时,图像会发生几何变形,如图1所示,在360°环形柱幕虚拟现实系统中,一系列投影仪分别将图像投射在不同的区域,计算机产生的均匀网格在投影幕上发生变形. 因此,虚拟现实系统不是简单地把投影图像拼接在一块就行了,必须进行几何校正,但是一般的投影仪无法实施几何校正.

图1 　360°弧形屏幕虚拟现实系统
Fig. 1 　A virtual reality system of 360°cylindrical screen

    1. 2 　投影仪与投影屏幕之间的几何关系计算方法

　　对投影仪产生的图像进行非线性几何校正之前,必须知道投影仪与显示屏幕之间对应的几何关系. 本文利用空间激光点阵确定屏幕上空间点的精确位置,并使用相机获取图像,经图像处理和特征提取后得到相机成像平面与投影屏幕的几何关系. 同样,通过投影仪输出规则的网格到屏幕上,得到相机成像平面与投影仪之间的几何关系,从而得到投影屏幕与投影仪之间的几何关系.

　　定义1 　假设投影幕与相机之间是透视投影关系,则可利用透视投影方程得到投影幕上3D 特征点[ x y z ]到相机图像空间对应2D 坐标[ u v ]的3 ×4 的透视投影矩阵Hsc . 即令n ≡[ uw vw w ]T 为相机图像空间对应点( w 为尺度因子) , m ≡[ x y z 1 ] T为投影幕空间对应点,则可得到透视投影方程

 　定义2 　假设投影仪与相机之间是透视投影关系,则可利用透视投影方程得到投影仪上2D 图像特征点[ u′v′]到相机图像空间对应2D 坐标[ u v ]的3 ×3 的透视投影矩阵Hpc . 即令n′≡[ u′v′1 ]T 表示投影仪图像空间对应点, n ≡[ uw vw w ] T 表示相机图像空间对应点,则可以得到投影仪到相机的透视投影方程为

　　定义3 　假设给定一个4 ×3 的透视投影矩阵Hps ,则投影仪与屏幕之间的透视投影方程为

　　利用定义1 和2 可以计算得到投影仪与投影屏幕之间的几何关系Hps .

    1. 3 　图像非线性几何校正

　　非线性几何校正的目的是对2D 投影图像进行变形,使观察者在屏幕上可观察到正常的透视投影图像[12 ] . 通过几何校正后, 帧缓存中的网格图像发生变形,而投影屏幕上的网格图像显示正常. 因此,对于需要几何校正的多投影仪拼接系统, 首先根据

    1. 2 节的定义计算投影屏幕与投影仪间的几何对应关系,推算帧缓存中图像的每个网格节点的目标位置,图2 所示为帧缓存中图像的原始网格与变形后网格的对应关系示意图. 然后逆算得到网格曲面的控制点网格. 下面是求解曲面控制点网格的方法.

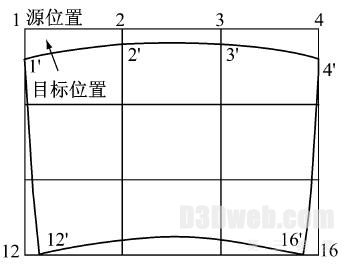
图2 　原始图像与目标图像的网格点对应关系
Fig. 2 　The relationship of regular grid and corrected grid

    文献[8 ]中,利用2 次曲面变换方法对投影图像进行几何变形,本文对投影图像进行双3 次曲面高精度实时几何变形. 常用的双3 次曲面有Bezier 曲面、B 样条曲面、非均匀有理B 样条(NURBS) 曲面,根据各种双3 次参数曲面的特性,考虑到视景图像的实时性和全局性要求,本文使用基于Bezier 参数的双3 次曲面对投影图像进行非线性几何校正.

    对于Bezier 曲面,设 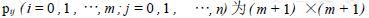为( m + 1) ×( m + 1) 的曲面控制点阵, Py 表示点阵中第i + 1 行、第j + 1 列坐标位置向量, Py =( Xy , Yy , Zy ) ,则m ×n 次Bezier 曲面定义为

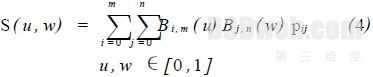
    式中:

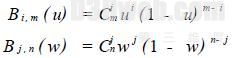
    均为Bernstein 基函数. 当m = n = 3 时,

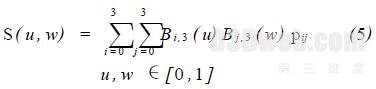
    则

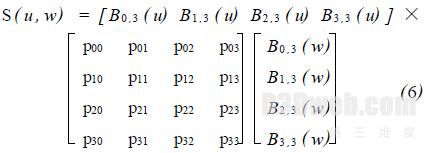
    其矩阵可表示为

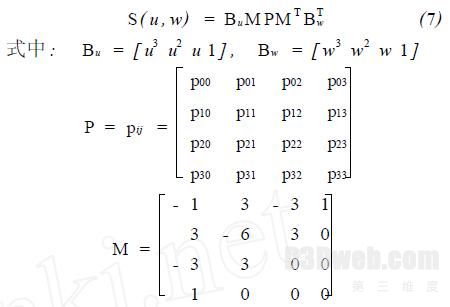
    利用广义矩阵法求取控制点阵P. 令Q = S ( u ,w) ,U = [ Bi ,3 ( u) ] ,W = [ B j ,3 ( w) ] , 则式(5) 可写成Q = UPW,根据Bezier 曲面的性质,U 和W 为正定矩阵,故其逆存在. 所以

    若考虑边界条件,U 、W 不一定是方阵, 则可用广义逆矩阵式求得

    本文设计了基于双3 次曲面算法的自动几何校正软件,水平方向选用7 个控制点,垂直方向选用5个控制点,即每个通道(每台投影仪) 分别由7 ×5 个控制点控制曲面形状,如图3 (a) 所示. 为了实现7 ×5 的控制阵列, 必须由4 个4 ×4 的双3 次曲面合成. 图3 ( b) 所示为通过校正后的控制点网格位置图,图3 (c) 所示为校正后的帧缓存中的变形图像.

    2 　投影图像边缘融合

　　在沉浸式虚拟现实系统中,通常采用水平视角3 通道(120°) 以上的弧形柱幕,3 通道是由3 台独立的投影仪产生的场景拼接在一起,如图4 所示. 拼接处不可避免地会有接缝,要想得到沉浸的虚拟现实效果,必须将通道之间的拼缝融合为一体. 本文给出了新的解决方法,在场景渲染时,直接对帧缓存中的图像进行实时亮度融合.

    2. 1 　投影图像边缘叠加

　　将相邻通道渲染的图像叠加一部分,通常叠加128 像素以上. 叠加像素数目可以不是2n ( n 为自然数) ,但是考虑到融合技术是基于OpenGL 和纹理映射方法对图像混合处理,2n 效率最高. 因此,融合宽度通常采用2n (见图4 中3 个投影通道叠加的效果图,中间呈现非常明显的2 条亮带) .

    2. 2 　边缘融合算法

　　将叠加部分图像的每个像素都乘上一个融合函数[12 ] ,即

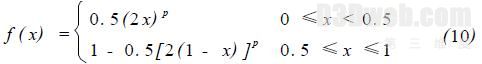
       式中: x 为像素列在叠加区的相对位置; p 为影响因子,函数曲线如图5 (a) 所示. 例如:右侧通道图像从左到右每列像素值乘上对应融合函数值,左侧通道图像从左到右乘融合函数1 - f ( x) ,图5 ( b) 所示为乘上融合函数后得到的图像.

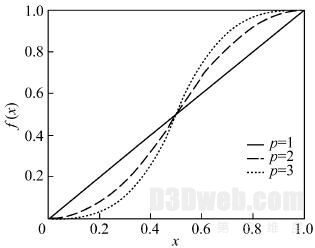
(a) 融合函数曲线

    (b) 投影图像乘上融合函数后生成的图像

(b) 投影图像乘上融合函数后生成的图像
图5 　边缘融合函数曲线与融合结果
Fig. 5 　The blending function and image blending result

    2. 3 　伽玛校正

　　如图5 (b) 所示,通过乘上融合函数后的图像并不完好,中间会出现2 条灰带,导致这种现象的原因是叠加区的图像仅仅增加像素值,没有对图像输出亮度进行改变. 因此,为了融合完整,必须将叠加区的像素映射成亮度的函数,即显示器的伽玛函数,如果G表示伽玛函数,则输出亮度就是像素值的G 次幂. 图6 (a) 所示为伽玛函数曲线图,图6 ( b) 所示为通过伽玛校正后的图像.

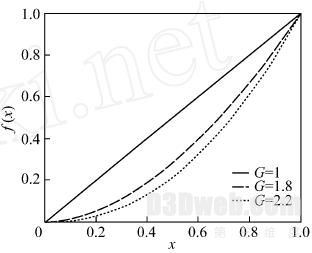
(a) 伽玛函数曲线

(b) 伽玛校正后的图像
图6 　伽玛校正
Fig. 6 　The Gamma calibration

    2. 4 　融合函数的优化

　　为了进一步控制叠加区图像的亮度,对式(10)进行修正,得到更加全面的边缘融合函数,即

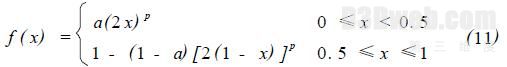
    式中, a 为亮度调节系数, a ∈[ 0 ,1 ] . 当a > 0. 5 时,则混合区的中心变亮;当a < 0. 5 时,则混合区的中心变暗. 图7 (a) 、( b) 所示分别表示a 取不同值时,得到的融合函数曲线图. 经过融合函数优化后,最终可以得到较好的融合图像,如图7 (c) 所示.

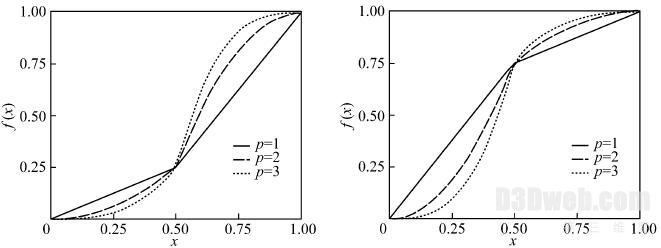
(a) a = 0. 25 融合函数曲线                           (b) a = 0. 75 融合函数曲线

(c) 图像融合结果
图7 　融合图像优化
Fig. 7 　The optimization of blending image

    3 　实验结果

　　本文介绍的算法适应于实时渲染的3D 虚拟现实系统. 实验步骤为:

    (1) 设定投影仪、相机以及投影屏幕位置,利用本文的自动非线性几何校正算法计算双3 次曲面的控制点阵,对实时渲染的图像帧进行几何变形;

    (2) 叠加区图像边缘融合.

    图8 (a) 所示为某一个投影仪图像的几何变形与融合结果,图8 (b) 所示为某虚拟现实系统的整体全景图. 通过实验,针对当前的普通商用投影仪,得到图像边缘融合参数的最优值区间: a ∈[ 0. 45 ,0. 55 ] , p ∈[ 1. 8 ,2. 8 ] ,G∈[1. 8 ,2 ,2 ] .

(a) 帧缓存图像                                 b) 某虚拟现实系统全景图
图8 　帧缓存图像与虚拟现实系统中的效果图
Fig. 8 　The images in f rame buffer and thevirtual reality system

    4 　结　语

　　随着虚拟现实技术与计算机图形学的快速发展,利用多投影仪拼接解决超高分辨率显示系统问题已经成为一种趋势,并且更多的投影仪拼接系统都是弧形柱幕和球幕,因此几何校正与边缘融合成了实现超高分辨率显示系统的关键技术之一. 本文结合工程实际需求,对非线性几何校正和融合方法进行了理论上的分析,并定义和计算了投影屏幕、投影仪与相机之间的几何关系,实现了图像的非线性几何变形;同时也解决了投影仪拼接处的边缘融合问题.

    参考文献:

    [ 1 ] 　Raskar R , Brown M S , Yang R , et al . Multi2projec2tor displays using camera2based regist ration [ C ]/ /Proceedings of IEEE Visualization. Los Alamitos :IEEE Computer Society ,1999 :161 - 168.

    [ 2 ] 　Raskar R. Immersive planar display using roughly a2ligned projector [ C ]/ / Proceedings of IEEE VirtualReality. New Brunswick : IEEE Computer Society ,2000 :109 - 116.

    [ 3 ] 　Raskar R , Beardsley P. A self correcting projector[C ]/ / Proceedings of Computer Vision and PatternRecognition. Kauai , Hawaii : IEEE Computer Socie2ty , 2001 :626 - 631.

    [ 4 ] 　Raskar R , Baar R , Beardsley P , et al . iLamp s : geo2met rically aware and selfconfiguring projectors [ C]/ /Proceedings of ACM SIGGRAPH. San Diego , Califor2nia :ACM Press , 2003 :809 - 818.

    [ 5 ] 　Ashdown M , Flagg M ,Sukthankar R , et al . A flexi2ble projector2camera system for multi2planar displays[C ]/ / Proceedings of Computer Vision and PatternRecognition. Washington DC: IEEE Computer Socie2ty ,2004 :165 - 172.

    [ 6 ] 　Okatani T , Deguchi K. Autocalibration of a projec2tor2camera system[J ] . IEEE Transanctions on PatternAnalysis and Machine Intelligence , 2005 , 27 ( 12 ) :1845 - 1855.

    [ 7 ] 　Okatani T , Deguchi K. Autocalibration of an ad hocconst ruction of multi2projector displays [ C ]/ / Pro2ceedings of Computer Vision and Pattern RecognitionWorkshop. Washington DC: IEEE Computer Socie2ty ,2006 :4 - 11.

    [ 8 ] 　Baar J , Willwacher T , Rao S , et al . Seamless multi2projector display on curved screens [ C]/ / Proceedingsof the Workshop on Virtual Environments. Zurich ,Switzerland : Elsevier Science ,2003 :281 - 286.
   
    [ 9 ] 　Song P , Cham T J . A theory for photomet ric self2cal2ibration of multiple overlapping projectors and camer2as [ C ]/ / Proceedings of the IEEE Computer SocietyConference on Computer Vision and Pattern Recogni2tion. Washington DC: IEEE Computer Society , 2005 :97 - 104.

    [10 ] 　黄永锋,李　杉,赵　军. 基于外标记点的2D/ 3D 图像配准方法[J ] . 上海交通大学学报, 2006 , 40 (7) :1108 - 1111.HUAN G Yong2feng , L I Shan , ZHAO J un. The reg2ist ration of 2D/ 3D images based on external makers[J ] . Journal of Shanghai Jiaotong University , 2006 , 40(7) :1108 - 1111.

    [11 ] 　Li K, Chen Y Q. Optical blending for multi2projectordisplay wall systems [ C ]/ / Proceedings of the 12thLasers and Electro2Optics Society. San Francisco :IEEE Computer Society , 1999 :281 - 282.

    [12 ] 　Bourke P. Edge blending using commodity projectors[ EB/ OL ] . (2004204208) [2007204210 ] . ht tp :/ / local.wasp . uwa. edu. au.