首先我们选取值最小的点作为参考点，将离散数据点按照它们与参考点之间的角度的大小对数组进行排序。其中选取x坐标最小点作为参考点有两个原因：①x最小的数据点必定是凸壳的顶点；②选取x最小的点作为参考点，可以使其它数据点与参考点之间的夹角在［-π2，π2］之间，在这个区间中，角度的正切值是随角度的增大而增大的，有利于编程实现。另外，我们使用离散数据数目加１的数组来存储数据点，并将排序后的数据点的第一点的坐标存入数组的最末位置上。

    int  Convex()

    { 假设凸壳顶点数目等于离散点的数目;

    j=1;

    for (k=3；k<＝凸壳顶点数目;k++)

    while (j

    { if (j+1点不是凸壳的顶点)

    { 删除该点，其后所有数据点前移一位;

    k=k-1;j=j-1;

    凸壳顶点数目减1;}

    else j=j+1;}

    return 凸壳顶点数目; }

    3．2  Bowyer-Watson算法的思想与实现

    Bowyer-Watson算法的基本思想：①假定已生成了连接若干个顶点的Delaunay三角网格；②加入一个新的节点，找出所有外接圆包含新加入节点的三角形，并将这些三角形删除，形成一个空腔；③将空腔的节点与新加入的节点连接，形成新的Delaunay三角网格；④调整数据结构，新生成的三角形的数据填充被删除三角形的数据，余者添加在数组的尾部；⑤返回第二步，直至所有的节点都加入为止。

    在初始网格的实现中，我们采用的是将凸壳看作是一个空腔，对其进行分割，形成一个符合Delaunay标准的初始三角网。再在此初始三角网格的基础上，应用Bowyer-Watson算法的思想生成最终的三角网。下面是该算法实现的伪代码（假定初始三角网已经生成）：

    void　Gernerate_Delaunay_Net( )

    { 初始三角形数组

    将所有待加入的离散数据点放入点堆栈中

    while(点堆栈不为空)

    { 初始化边列表为空;

    点堆栈进行出栈操作，即弹出一个待加数据点;

    for (i=0;i<三角形数组中元素的个数;i++)

    { 计算三角形的外接圆的圆心和半径；

    if (待加数据点在三角形的外接圆内)

    { 将该三角形的三条边与边列表中的所有边进行比较；

    { if (该边已经在边列表中存在)
   
    边列表中的这条边的权值变为2；

    else if (该边不在边列表中)

    则将该边加入边列表;}

    将该三角形从三角形数组中移出;}

    for (i=0;i<边列表的长度；i++)

    { if (边的权值为1)

    { 将边与待加数据点形成的所有三角形加入到三角形数组中;

    }}}}

    4  实验结果与分析

    对于前述算法，笔者已经用VC++6.0在计算机上实现，实验表明对于TIN模型的生成，该算法是行之有效的。在图１中展示了离散点生成Delaunay三角网的实验结果。以上实验结果，实际上只是地形可视化研究的基础工作，在以后还将涉及到大量数据的试验。造成这样结果的原因是由于数据来源的限制，因此，在我们的实验结果中并非是直接针对实际地形数据做出的模拟；只是一些由笔者自行输入的几十个点数据，目的旨在验证算法的有效性和可行性。对于大幅地形图而言，由于数据的采集量很大，一般都在上万个数据点以上，与这样的数据量相比，实验中所涉及的数据量显然是很小的。实验结果表明，用小数据量的离散点来生成Delaunay三角网时，算法能得到很好的结果；而对于大数据量而言，算法的效率可能会很低，这取决于在计算过程中所生成的三角形的数目。假定输入离散点的数目为n，生成一个由m个顶点构成的凸壳的时间复杂度为O（n logn），生成初始三角网的时间复杂度为O（n2），这期间将对初始三角网进行调整，使其符合Delaunay法则，需要对至多（3n-6-m）条边的搜索，其时间复杂度为O(n)，插入点时间复杂度约为O（n2），那么该算法总的时间复杂度约为［O（n2）+O(n)+O（n2）］，即O［2n（n+1）］.

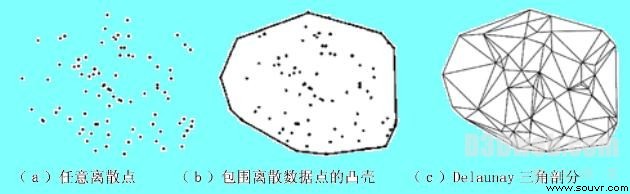
图１ 由任意离散点生成Delaunay三角网格

    5、结束语

    今后，我们将针对海量的实验数据、特征线、特征点等问题，对算法程序进行完善和修改，此外还将对TIN模型，即Delaunay三角网的三维显示进行研究。