摘  要：本文分析实现真三维GIS的技术难点，从2.5维GIS可视化基础出发，选用TIN模型作为地形可视化的数据模型，介绍了程序中所采用的TIN模型的拓扑数据结构，并以凸壳技术和Bowyer-Watson算法的思想为基础，实现一种由任意离散点生成Delaunay三角网格的算法。

    引  言

    计算机软硬件的发展水平一直是制约地理信息系统（GIS）发展的主要问题之一，特别是三维可视化方面的研究。近年来，虽然计算机的数据处理能力以及图形显示能力已经大大提高，但对于真三维的地理信息系统的实现而言，仍然存在诸多尚未解决的技术难点。

    首先，空间三维数据的采集，其成本相当昂贵；

    其次，真三维GIS的空间数据量大，种类多，结构复杂；

    第三，三维空间的点、线、面和体之间的拓扑关系复杂，技术尚不成熟；

    第四，空间分析困难。

    因此，在地理信息的三维可视化（特别是地形三维可视化）的研究中，通常采用2.5维的GIS可视化的方法来实现地理信息的三维可视化。该方法主要是以高质量的数字高程模型（DEM）和高逼真度的三维显示技术为基础。其中DEM的质量，对地形三维可视化的效果有着不容忽视的影响；而影响DEM质量的关键是生成DEM的算法。所以，采用一种实用性强、精度较高、生成速度快，使用方便的DEM的生成算法是十分必要的。

    1  数字高程模型

    在地理信息中，DEM主要有三种表示模型：规则格网模型（Grid）、等高线模型和不规则三角网模型（Triangulated Irregular Network，TIN）.但这三种不同数据结构的DEM表征方式在数据存储以及空间关系等方面，则各有优劣，见表１.

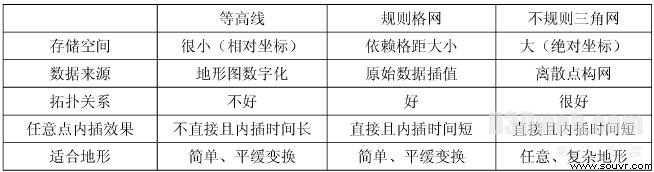
表１  不同数据结构数字高程模型的比较

    从表１我们可以看出，虽然TIN在存储空间的要求上相对较高，但在处理任意复杂的地形上具有绝对的优势，加之大多数图形显示硬件都针对三角形进行了特殊优化；因此，在可视化研究中以TIN的数据结构作为我们研究的数据模型。

    生成DEM的数据通常以矢量化的等高线和其它特征点、线数据或者直接从各类矢量数据库中取出的等高线矢量数据为主要数据源。这些数据从数字化仪获得，主要以离散点为主。对于离散点转换成TIN，最常用的方法是Delaunay三角剖分法，选用一种合适的算法来生成Delaunay三角网是我们研究的主要目的。

    2  ＴＩＮ的数据结构

    考虑到生成TIN的算法中点、线、面之间的拓扑关系，我们采用了如下的数据结构作为TIN的存储结构。该数据结构能够较好的建立TIN数据模型的拓扑关系，并且能在其点、边以及三角形之间建立快速索引，有利于我们在TIN生成算法中的实现，具体如下。

    2.1  离散点表

    离散点表作为所有点坐标数据的数据库，建立其索引便于以后的边表和三角形表中点索引的查询。

    class DiscretedPoint：public Object

    ｛ float x，y;// 离散点的坐标

    int index;//点的索引 ｝

    2.2  有序边表

    记录三角网生成期间所使用过的边，以及最后存储的三角形间边的信息。

    class Edge：public Object

    ｛int Start;// 边的起点

    int End;//边的终点

    int LeftTriangle;// 边的左三角形索引

    int RightTriangle;// 边的右三角形索引

    int index;// 边的索引｝

    2.3  三角形网表

    记录最终生成的TIN数据模型中的三角网之间的拓扑关系。该数据结构是以经典的LTL（Lawson's Triangle List）表结构来存放三角网信息的。

    class TriangleNet：public Object

    ｛int NodeA;// 三角形的顶点A的坐标索引

    int NodeB;// 三角形的顶点B的坐标索引

    int NodeC;// 三角形的顶点C的坐标索引

    int AdjTriangleA;// 三角形的顶点A的对边相邻的三角形

    int AdjTriangleB;// 三角形的顶点B的对边相邻的三角形

    int AdjTriangleC;// 三角形的顶点C的对边相邻的三角形

    int index;// 三角形的索引｝

    3  ＴＩＮ的实现

    我们所采用的Delaunay生成算法主要分为两步：首先要生成一个包括所有离散数据点的凸壳；再利用该凸壳生成一个初始的三角网，并在此基础之上，逐个加入其它离散点，生成最终的三角网。对于凸壳的生成我们采用格雷厄姆算法，该算法是求解平面点集凸壳问题的最佳算法，算法复杂度为O（n logn）.对于三角网上加入其他数据点的算法是基于Bowyer-Watson算法的思想，该算法能很好的生成符合Delaunay法