胡海昌^[1]，中国现代固体力学家、中国空间技术研究院研究员。创立了弹性力学三类变量广义变分原理，即国际上公认的胡－鹫津原理；建立了力学上新型的边界积分方程；首次找到了横观各向同性弹性体空间问题的一些重要解。在振动理论和结构理论方面也有重要贡献。
　　胡海昌1954年在《物理学报》发表论文《论弹性体力学与受范性体力学中的一般变分原理》，提出固体力学中的三类变量广义变分原理。这一原理推广了最小势能原理，是用位移、应变和应力为自变函数的一种无条件变分原理。日本人鹫津久一郎(1921～1981)比他晚一年独立地重建了上述原理。由于它在有限元法和其它近似解法的重要应用，后来受到美、日、英、苏、德、法等多国的学术文献、专著、教科书广泛介绍和引用，并称之为胡－鹫津原理。胡海昌还写有科学论文《横观各向同性弹性力学的空间问题》(1953)、《在均布及中心集中载荷作用下圆板的大挠度问题》(1954)、《广义变分原理在近似解中的合理应用》(1982)等50多篇以及专著《弹性力学的变分原理及其应用》(1981)等。

生平

　　胡海昌，1928年4月25日出生于浙江省杭州市的一个从事教育工作的小知识分子家庭。1946年考入浙江大学土木工程系，学习刻苦，且自学有方，善于从理论角度分析问题。他深受当时在浙江大学任教的钱令希的赏识，因而得到其特殊指导，在大学期间就完成并发表了两篇学术论文。
　　1950年大学毕业后，他进入中国科学院数学研究所力学研究室工作，从此开始了从事力学研究的生涯。在钱伟长领导下，力学研究室是一个非常活跃的研究集体。刚迈出大学校门的胡海昌，在短短几年内就在弹性力学、板壳理论等领域发表了约30篇论著。其中尤为重要的是发表于《物理学报》（1954年10卷2期）上的《论弹性体力学和受范性体力学中的一般变分原理》。该文创立了三类变量广义变分原理，对弹性力学、变分原理、力学中的数值方法产生了深远影响，被世界公认为胡－鹫津原理”。
　　1956年，中国科学院力学研究所成立，胡海昌任该所助理研究员。同年，他参加的以钱伟长为首的集体研究成果《弹性薄板的大挠度问题》获中国科学院自然科学奖二等奖。以后，直至1965年，胡海昌一直在中国科学院力学研究所工作，任副研究员、固体力学研究室主任，从事早期的火箭总体设计和壳体稳定性研究。
　　60年代初，我国集中了一批优秀专家研究空间技术。1966年，胡海昌到中国空间技术研究院空间飞行器总体设计部工作，历任空间飞行器总体设计部副主任、科技委员会主任、名誉主任等职，1981年被聘为研究员。胡海昌在运用理论知识解决实际问题、指导工程技术工作的同时，仍坚持从事理论研究，不断取得新的成果。
　　1981年，胡海昌当选为中国科学院学部委员。
　　在从事科学研究的同时，胡海昌还热心于教育事业。从50年代起，他在北京大学数学力学系讲授弹性力学、板壳理论、薄壁杆件理论、弹性力学中的变分原理、振动理论等多门课程，还在清华大学、中国科学技术大学、北京航空航天大学等校兼职，并自1957年起，开始指导研究生。自1979年起，任北京大学、浙江大学兼职教授、首批博士生导师。
　　胡海昌还担任了国务院学位委员会力学评议组成员、中国振动工程学会理事长、中国气功科学研究会学术委员会副主任、《振动工程学报》主编等职。曾任中国力学学会第一、第二、第三届理事，第三届副理事长，现任名誉理事；《力学学报》副主编、《振动与冲击》主编等职。
　　1978年以后，还先后担任北京市第五、第六、第七、第八届政治协商会议委员，全国第八届政治协商会议委员。

成就

　　

1创立三类变量广义变分原理

　　　胡海昌除了进行有关我国空间飞行器的研究、设计工作以外，曾发表论文百余篇，涉及弹性力学、塑性力学、流体力学以及结构力学的平衡、稳定和振动等领域；还有著、译7本。他的研究工作极富创造性，尤其在广义变分原理方面的杰出成就，是对力学的重要贡献，在国际力学界产生很大影响由于工程中的力学问题大多难于求得精确解，因此寻找其简单可行而又有实用精度的近似解成为力学界长期探讨的课题。
　　50年代以前，各种重要的近似解法大致可分为三类：第一类是根据力学背景作出若干简化假设，建立工程实用的结构理论。从固体力学观点衡量，这些近似理论大多精确满足连续条件和平衡条件而近似满足本构关系，例如梁、板、壳理论。第二类是根据最小势能原理用里兹法求近似解。它们虽能精确满足连续条件和本构关系的要求，但只能近似满足平衡条件。第三类是根据最小余能原理用里兹法求近似解。它们虽可精确满足平衡条件和本构关系，但只近似满足连续条件。
　　还在大学期间，胡海昌就在钱令希的指导下开始探索这一课题，力图求得一种方法，它不强制要求精确满足什么方程，而是把哪些方程能精确满足，哪些方程能近似满足的问题留给解题人根据问题的性质来作出抉择。1950年E．H．莱斯纳（Reissner）提出了弹性力学的二类变量广义变分原理，展示了在能量法中同时近似地满足不同力学性质的方程的可能性。继而，胡海昌于1954年在《物理学报》上发表了《论弹性体力学和受范性体力学中的一般变分原理》，文中提出了三类变量广义变分原理。在这个变分原理中，位移、应变和应力三类变量全都作为自变函数，全部方程都不必精确满足。这是一个无条件的变分原理，它为以往的工程实用结构理论提供了能量法观点的解释，更为研究各种近似解法提供了空前灵活的理论根据。
　　这篇论文发表后，在五六十年代，国内掀起了研究变分原理的热潮。一方面是根据广义变分原理用里兹法求近似解，这在国际上是一个创举，比国外同类工作早了5年。另一方面是相继提出了板、壳、振动、稳定诸问题的广义变分原理，在国际上也处于领先地位。
　　1964年，美国同行率先把胡海昌提出的变分原理称为胡鹫津原理（鹫津久一郎，日本人，1955年在美国提出与胡相同的变分原理）。1970年前后，不断有人指出，广义变分原理是建立包括有限元法在内的各种近似解法的坚实的理论基础。这样，在国外也出现了研究和利用变分原理的热潮，尤其是根据广义变分原理来论证已有的和建立新的有限元法。自此，胡－鹫津原理得到美、日、苏、英、法、德、意等国同行的公认，并在众多的弹性力学、板壳理论、有限元法的专著和论文中得到介绍和引用。一项国内的力学研究成果在国外引起如此强烈的反响，尚属罕见。
　　1982年，以胡海昌为首的5位力学家的研究成果《弹性力学的广义变分原理的研究》获国家自然科学奖二等奖，他的专著《弹性力学的变分原理及其应用》获全国优秀科技图书奖。

　　

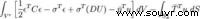
2建立新型的边界积分方程

　　　60年代以后，边界积分方程和边界单元法逐步兴起，现在它已和有限元法、加权残差法、差分法并列为计算力学中的4大方法。数学中的第二类积分方程便于数值求解，而第一类积分方程较差。以前，边界积分方程属于哪一类，取决于问题中边界条件的性质，而不取决于解题人的愿望。