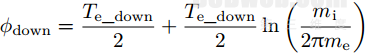多模式离子推力器栅极系统三维粒子虚拟现实仿真
来源:第三维度
作者:陈茂林,夏广庆, 毛根旺
单位:西北工业大学
(固体火箭发动机燃烧、
热结构与内流场国防科技重点实验室)
大连理工大学
(工业装备结构分析国家重点实验室)
摘要:栅极系统是离子推力器推力产生的主要部件, 推力器的性能和寿命都与栅极系统密切相关. 对于具有多种工作模态的离子推力器, 基于电流电压入口的仿真可以有效评估推力器的工作状况. 采用三维粒子模拟方法对两栅极系统等离子体输运过程进行了仿真, 获得了不同模式下的推力器性能参数, 对比NSTAR的在轨测试参数, 验证了模型的正确性; 分析了工作模式变化对栅极区域电场分布和束流状态的影响以及离子推力器多模式设计需求. 分析结果表明: 远离栅极系统的外凸型屏栅鞘层和内凹型零等势面、低鞍点电势值和平缓的下游电势分布, 有利于提高栅极系统离子通过率, 抑制电子返流, 减小Pits-and-Grooves腐蚀, 是离子推力器工作模式的设计方向; 提高束流电压会导致发散角损失增大, 但可扩展栅极工作电流范围, 在束流强度较大的模式下, 使束流具有较好的聚焦状态, 有利于减小Barrel腐蚀. 研究结果为多模式离子推力器工作模式设计提供了参考。
1 引 言
20世纪90年代以来, 以XIPS-13, XIPS-25,NSTRA-30, T6和-10为代表的离子推力器实现了航天器姿轨控动力的大规模应用[1−3]. 随着航天技术的发展和任务的多样性需求, 多模式工作逐渐成为离子推力器主流设计方向, 其中NASA的NSTRA-30便具有112种工作模式[4], 兰州空间技术物理研究所正在研制的LIPS-300离子推力器也设计了大、中、小三种典型的推力模式。
由于栅极系统是离子推力器产生推力的主要部件, 栅极系统的正常工作与否决定离子推力器的性能和寿命. 由于栅极系统实验成本和周期过长等因素, 研究人员针对离子推力器栅极系统开展了大量的仿真工作。 1979年, 美国橡树岭国家实验室便开始了离子推力器栅极系统的粒子模拟(PIC)仿真研究[5, 早期的工作主要是二维的模拟, 研究栅极系统的电场分布和离子束流运动轨迹; 近年来,大量关于栅极系统的PIC仿真工作重点集中在新型高精度算法的研究、栅极腐蚀的模拟、电子返流、截止电流以及负离子引出过程的模拟, 以期为后续高效、长寿命、多模式栅极系统的改进设计提供参考依据[6−9]; 弗吉尼亚理工大学的Lin和Wang提出了离子推力器栅极模型的浸入式有限元求解方法; 密西根大学的Emhoff建立了NEXT离子推力器的二维栅极腐蚀模型; 科罗拉州立大学开发了用于离子推力器栅极仿真的三维柱坐标igx程序和ffx程序, 并采用ffx对NASA的大功率电推进计划离子推力器的栅极系统进行了仿真; 北京航空航天大学Zhong等[10]、刘畅等[11], 哈尔滨工业大学杜军[12], 西北工业大学孙安邦[13], 兰州空间技术物理研究所贾艳辉等[14] 分别开展了离子推力器二维/三维PIC的仿真研究工作, 计算了不同推力器栅极系统的屏栅透明度、离子引出路径等与性能评价相关的参数和加速栅溅射腐蚀、屏栅溅射腐蚀等与寿命评价相关的参数。
上述研究工作主要是针对某一固定工作模式下的栅极系统, 对于多模式的栅极系统的仿真研究, 特别是多模式栅极系统工作模式设计的分析未见报道。
本文针对多模式离子推力器栅极系统, 开发了三维PIC仿真程序, 针对多模式需求, 改进了栅极入口条件设置. 以30 cm NSTRA离子推力器为仿真对象, 模拟了不同模式下的电势分布和离子运动状态, 从鞘层结构、下游零等势面位置、轴线电势分布、离子撞击加速栅几率、屏栅离子通过率、发散角损失等方面分析了工作模式设计过程中需要考虑的问题, 研究结果可为多模式离子推力器工作模式优化设计提供理论指导。
2 模型及模拟过程
2.1 仿真区域
由于栅孔结构的对称性, 仅取1/4个栅孔区间作为计算区域, 如图1所示. 图1 (a)是单个完整栅孔的三维结构, 计算区域取为ABCD-A′B′C′D′;图1 (b) 为计算区域的左视图; 图1 (c)为计算区域的对称结构; 图1 (d)为单孔完整视图。
图1 计算区域 (a)三维空间结构; (b)左视图; (c) 对称结构; (d) 完整视图
根 据 栅 极 结 构 尺 寸, 对 计 算 区 域 进 行 结构 化 网 格 划 分, 考 虑 放 电 室 等 离 子 体 密 度 在, 网格空间步长取为。
2.2 PIC/MCC模型
PIC方法是模拟低温等离子体的一种常用数值方法, 它是粒子的运动和自洽电场的耦合求解方法[15;16]。 蒙特卡罗碰撞(Monte Carlo collision,MCC)是用来描述粒子间碰撞的常用方法, 本文用MCC方法来求解带电粒子与中性粒子间的碰撞。
2.2.1 离子的运动
离子的运动遵循牛顿-洛仑兹定律, 其运动方程如下:
2.2.2 电子数密度
对于电子而言, 其质量较轻、运动速度较快, 若采用粒子描述, 其时间步长的选取要比离子低约三个数量级, 大大增加了计算量. 因此, 本模型假设电子为流体, 数密度服从Boltzmann分布. 模型中电子主要由以下两部分组成, 一是上游放电腔鞘层区域内的高能电子, 二是下游羽流区域中和器发射出的中和电子。
在屏栅孔及其上游区域:
其中n0, ϕ0和Te0分别为上游放电腔内等离子体考数密度、电势以及温度。
在加速栅下游区域:
其中n∞, ϕ∞ 和Te∞ 分别为下游羽流区域等离子体参考数密度、电势以及温度。
2.2.3 电场求解
电场由泊松方程求解:
将Boltzmann方程和泊松方程耦合求解, 即有
对上式进行线性化处理[12] 后, 可用超松弛迭代(SOR)方法进行求解。
2.3 边界条件
2.3.1 入口边界
如图1所示, ABCD为入口边界面. 根据鞘层理论, 取入口处离子进入速度为Bohm速度, 即
入口离子数密度和离子通量常常根据放电室等离子体密度计算[3;5;11−13], 本文考虑到多模式的工作情况, 以及放电室等离子体密度的空间分布差异, 采用离子推力器束流J 作为入口条件来计算离子数密度和离子通量, 得到的结果可更方便地进行验证。
对应的单个栅孔的离子束流为
式中, AABCD为计算区域入口面面积, 也即半个栅孔对应的入口面积; AG为有效栅极面积。
由此, 可得入口处的离子数密度为
η为屏栅的离子通过率, 一般为0.85—0.90之间, 可先设为0.85后, 通过仿真结果进行调整。
对应放电室等离子体密度, 即上游参考等离子体密度为n0 = ni/0.605; 上游参考等离子体电势为ϕ = ϕsc + ϕp ϕw, ϕsc 为屏栅电势, 为壁面相对于预鞘的电势,ϕp = Te /2为预鞘的电势降, 即等离子体内部与预鞘边界之间的电势差.
2.3.2 出口边界
如图1所示, A′B′C′D′为出口边界面. 出口边界面电势按下游等离子体电势取
Te_down为下游电子温度。
A′B′C′ D′ 的粒子边界条件为: 当离子运动离开出口边界时, 按逸出处理, 删除粒子信息。
2.3.3 对称边界
如图1所示, AA′BB′, AA′DD′, BB′CC′, CC′DD′为对称边界面.
对称边界面上, 沿对称面法向电场为0, 即AA′BB′ 和 CC′DD′ 面上, Ey = 0; AA′DD′ 和BB′CC′面, z = 0; 对称面交界线AA′, BB′, CC′ 和DD′面上, Ey = 0, Ez = 0。
对称边界上的粒子处理方式为: 当离子运动越过对称面, 按镜面反射处理。
2.3.4 固壁边界
栅极系统为计算中的固壁边界, 对于栅极固壁, 电势为恒定值Vsc, Vacc; 栅极内部电场为0。
粒子的固壁边界为: 当离子撞击到栅极表面时, 按吸收处理, 即删除粒子信息。
2.4 算例与模型验证
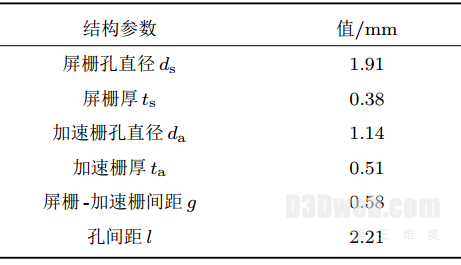
本文采用NASA的30 cm NSTAR离子推力器栅极结构作为计算依据, 栅极结构参数见表1。
表1 栅极结构参数
.
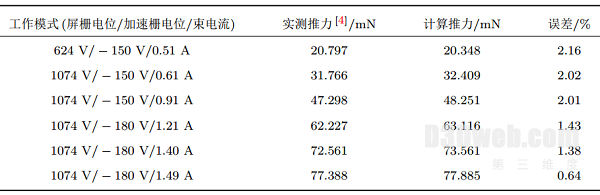
计算了不同工作模式(电流/电压)下的推力, 并与NSTAR在轨实测结果进行了对比, 如表2所示。
由表2可以看出, 采用本文仿真模型计算出的推力值和在轨测量值基本一致, 验证了仿真模型和数值方法的准确性。
表2 仿真结果与NSTAR实测结果对比
首页 上一页 1 2 3下一页尾页 共3页







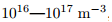 , 网格空间步长取为
, 网格空间步长取为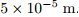 。
。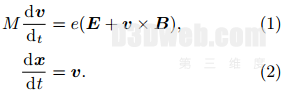
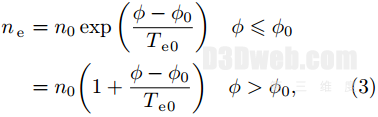
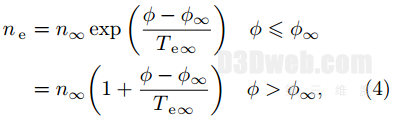

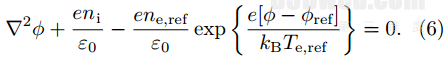

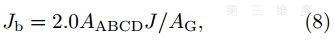
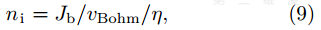
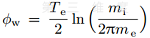 为壁面相对于预鞘的电势,ϕp = Te /2为预鞘的电势降, 即等离子体内部与预鞘边界之间的电势差.
为壁面相对于预鞘的电势,ϕp = Te /2为预鞘的电势降, 即等离子体内部与预鞘边界之间的电势差.