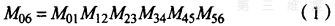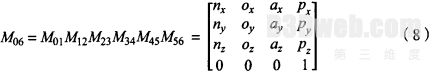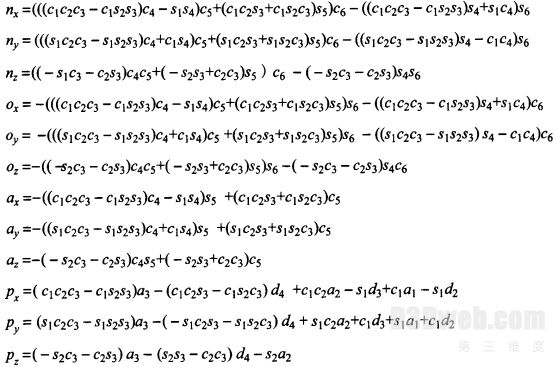来源：第三维度
    作者：邢迪雄，张琦
    单位：华北电力大学，河北保定071003

    摘要：机器人三维运动仿真是当前机器人研究领域中重要的研究方向之一。利用高端三维CAD软件对六自由度M 6iB机器人建立三维运动仿真模型。采用D—H参数法建立了连杆坐标系下的机器人运动学模型。并利用Matlab编写了运动学方程的变换矩阵，最后利用软件对机器人的运动进行分析。研究了运动学方程的求解，基于CATIA V5的DUM中的部分模块，对工业机器人运动学进行仿真，并对仿真进行结构、干涉和碰撞等分析，验证出各关节角运动函数的正确。

    工业机器人运动学是机器人学的一个研究领域，是机器人系统的基础。以工业上常见的关节式机器人为例，机器人实际上可视为由一系列关节连接起来的连杆组成，把坐标系固定在机器人的每一个连杆的关节上，可用齐次变换来描述这些坐标系之间的相对位置和位姿方向(简称位姿)。齐次变换既有较直观的几何意义，又可描述各种杆件之间的关系，所以常用于解决运动学问题。运动学问题是研究机械手末端执行器(即手部)相对参考基准的位置、姿态和速度与各关节位置和速度之间的关系，包括运动学正问题和运动学逆问题。

    运动学正问题(Direct KinematicProblems，DKP)：给定机器人手臂、腕部等构件的几何参数及连接各构件运动的关节变量，求机器人末端执行器对于参考坐标系的位置和姿态。参考坐标系为固定在大地上的笛卡尔坐标系，作为机器人的总体坐标系，也称为世界坐标系(World Coordinate)；目前运动学正问题的研究主要是利用齐次坐标变换矩阵方法将位置和姿态统一描述，该法思路清晰，但运算速度较慢。随着机器人机构自由度的增加对运动学逆问题的讨论带来很多不便。

    运动学逆问题(Inverse KinematicProblems，IKP)：已知机器人各构件的几何参数和机器人末端执行器相对于参考坐标系的位置和姿态，求解关节变量的大小。机器人动学逆问题是编制机器人运动控制系统软件的基础。运动学逆问题比正问题复杂的多，主要表现在逆解的存在性和非唯一性，存在性决定机器人的操作空间，逆解一般来说非唯一。

    目前对具有特殊形状的机器人机构如球形手腕机器人机构，其逆解是闭式的，但是不唯一。对一般的机器人机构逆解必须使用数值计算方法，因而数值解的计算速度和精度受到人们的关注，同时机器人机构中常见的奇异状态(不可解状态)在数值解中如何避开也是讨论问题之一。

    1 机器人本体结构简介及数学模型的建立

    1.1 机器人本体结构简介

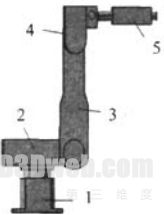
    本文以M一6iB机器人为研究对象的六自由度工业机器人，其建立的实体模型如图l所示。具体关节结构由回主体具体关节结构由回转主体(腰关节)、大臂(肩关节)、小臂(肘关节)、腕部(腕关节)等几个部分组成。机器人回转主体实现机器人主体的回转，由固定底座和腰关节组成，驱动电机l安装在腰关节的轴中心，驱动腰关节的回转。电机2安装在大臂与小臂的关节连接处，驱动小臂作上下俯仰。机器人的腕部位于小臂臂体前端，安装在小臂臂体上的电机3驱动整个腕部做上下俯仰。腕部的三个自由度由安装在腕部后端的3个电机，通过传动杆驱动腕部齿轮系实现，安装在腕部后端的3个电机保证机器人末端重量尽可能的轻，满足机器人的配重法则。

1.基座2腰转部件3.大臂4.小臂5.腕部
 图1 M一6iB机器人实体模型

    1.2 机器人运动学数学模型的建立

    机器人运动学分析常用的方法是D—H参数法，是由Denavit和Hartenberg于1955年提出的一种为关节链中每一杆件建立附加坐标系的矩阵方法，是用齐次坐标来描述机器人各连杆相对于参考坐标系的空间几何关系，用4X4的齐次变换矩阵来描述相邻两连杆i和f—l的空间几何关系，从而推导出机器人手爪坐标系相对于参考坐标系的空间位姿关系。

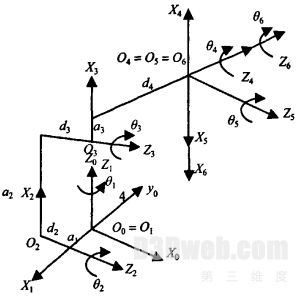
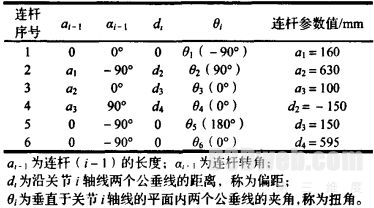
    本文分析的六自由度工业机器人由基座、腰转部件、大臂、小臂和腕部组成，具有六个转动自由度，根据D—H坐标系的规则和各杆件参数的求取规则，建立了机器人处于零点位置时的连杆坐标系，如图2所示。表l列出了机器人机构的D—H参数。

图2M 6iB机器人的连杆坐标系

表1 M 6iB机器人的D—H参数

    2 工业机器人运动学方程

    运动学方程的建立与求解是一个机器人系统的关键技术。建立杆件的D—H坐标系，就可以确定联系i坐标系和i—I坐标系的齐次变换矩阵。根据齐次坐标变换理论，可知工具坐标系是从基坐标系到各个杆件坐标系之间的变换得到的。即：

    式(1)是机器人正向运动方程，其中吁。一lb为相邻于间的位资矩阵，诋为机器人末端执行件的位资矩阵。下面就用D—H方法求解运动学正解。根据齐次变换原理和位姿理论得到各关节的位置矩阵如下：

    将以上连杆的齐次变换矩阵导入Matlab 软件中计算就得到操作臂变换矩阵

    式中：cf，曲分别表示cosoi，sinOi。当将各关节角的初始位置，即口l=一90。，02=900，03=0。，04=0。，05=180。，06=OO的值代入上述表达式中，可得：nx=0，ny=0，他=1，Ox=l，Oy 20，Oz=0，ax=0，ay=1，吃=0，Px=0，pv=al+d4，见=a2+a3，与以基位姿为参照手部位姿的矩阵相同，即运动方程是正确的。

    3 机器人模型运动仿真及分析

    3.1 机器人模型运动仿真

    在CATIA V5软件环境下，对机器人进行运动仿真之前，先要在CATIA V5的DMUKinematics(数字模型运动分析)模块中装配机器人并为机器人模型各关节建立驱动命令，此模型中 Revolute(旋转接头)建立零件间的旋转自由度的旋转接头，利用；纛iFix rod(固定零部件)建立约束。按照实际情况对各关节建立转动接头或约束，然后为各关节的运动参数确定其变化函数。在本文讨论的实例中，此函数即为各关节角的运动学逆解，完成这些工作之后，便可以让机器人模型进行运动仿真以观察其运动情况，例如运动中有无干涉、手部运动轨迹如何等。其仿真运动的基本状况如图3所示。

    3.2 运动仿真分析

    首先对机器人的三维实体进行运动机构仿真分析，分析结果如图4所示。从图4中我们可以看出运动学机构中的所有约束的名称、类型以及所连接的组建等详细信息，换可以看到那些约束被分配了驱动命令。

图4 运动结构分析

    然后对机器人进行运动碰撞检查，如图5所示。从图中可以看出大臂和腰转部件发生了不相关的碰撞，其余各零部件间没有发生碰撞。

图5 运动碰撞检查

    从机器人模型的运动仿真过程看，没有出现运动干涉和碰撞，说明各部件的造型和装酉己是正确的，另外各关节角在运动中转动都很正常，使机器人手部的运动轨迹可以触及到其运动空间的任意点，说明各关节角运动函数正确。

    4 总结

    本文首先建立了机器人的连杆坐标系，对机器人运动学方程的正解和逆解进行了具体的推导和求解，通过CATIAV5软件，对M一6iB型机器人进行运动学仿真通过三维实体建模，运动仿真和分析以验证各关节角运动函数的正确性，为后续机器人的轨迹规划及运动，静态分析提供了可靠性。

    参考文献：

    [1] 吴瑞祥.机器人技术及应用[M].北京：北京航空航天大学出版社。1993.

    [2] 尤春风.CATIA V5高级应用[M].北京：清华大学出版社2006.

    [3] 鲁君尚，张安鹏，等.CATIA V5之电子样机[M].北京航空航天大学出版社，2008.

    [4] 杨达毅.6R型工业机器人的运动学研究[D].吉林：吉林大学，2005.

    [5] 李庆龄。刘加亮.六自由度工业机器人运动学分析及仿真[J].机电工程技术。2008(37)：36—38.

    [6] Vingrodov.Features of the Kinematics of Manipulators andVolumes Methods[R].US Grovemment Technology Report，2004.

    [7] 薛红军，任雅广，刘振宇.基于UG二次开发的工业机器人作业仿真系统设计[J].机电工程。2010，27(6)：52—55.