来源：第三维度
    作者：康 玲, 王学立, 明 博
    单位：华中科技大学水电与数字化工程学院

    摘要: 根据不规则三角网生成算法的最新研究成果, 改进了递归分割- 合并算法, 并针对目前三角网生成算法的缺点, 提出了包络三角网生成算法. 根据 GPS 实测数据生成不规则三角网, 实现了水下地形的可视化. 应用实例表明, 包络三角网生成算法有效地减少了冗余三角形的生成, 生成的三角网与实际湖底形状吻合较好.

    当前, 我国很多湖泊水库存在着不同程度的底泥污染物淤积问题, 造成湖泊水库容量减小, 削弱了其对污染的稀释自净能力和自身的承载能力. 对湖泊水库进行环保疏浚可以清除作为内源污染的底泥, 增加库容, 改善水生态环境. 传统的机械疏浚, 单纯地以航道疏通、水体增容为目标, 不能满足当前对生态环境保护的需求. 环保疏浚要求在完全清除底泥的同时, 避免破坏底质原生土, 并减少底泥扰动和污染物的二次扩散[1-2]. 因此, 环保疏浚要求严格控制挖深, 精确疏浚. 获取底泥的精确地形数据、实现水下地形可视化则有助于实现精确疏浚. 本文利用离散实测底泥数据生成三角网, 实现了水底地形的精确可视化.

    1 不规则三角网生成算法

    针对如何高效生成不规则三角网( irregular triangle network,TIN) , 已有许多研究[3-6], 主要出现了分治、逐点插入与三角网成长 3 类算法[7]. 数据量大时, 纯粹使用单一算法, 会消耗大量的时间和空间. 于是, 一些学者结合分治算法与逐点插入算法, 提出了自适应递归分割三角网合并算法.

    自适应递归分割三角网合并算法的思想是: 首先设定分割阈值, 根据分治算法对目标数据集进行递归分割. 当分割后的子集小于阈值时, 分割完成. 然后对子集逐点插入生成子三角网. 当子三角网生成完毕后, 再递归合并子三角网, 实现整个点集范围内的三角网生成[8-9].

    本文主要讨论子网合并算法. 目前的子网合并算法, 一般使用递归过程来生成间隙三角网, 不能顺序构造三角形, 也没有对生成的三角网进行合法性判断. 本文利用一个简便的方法判断新构造三角网的合法性.

    首先, 在构造间隙三角网时, 新生成的三角形的边与相邻凸壳顶点一定存在 3 种关系: 反射、支撑、凹[10], 分类限制条件如图 1 所示. 

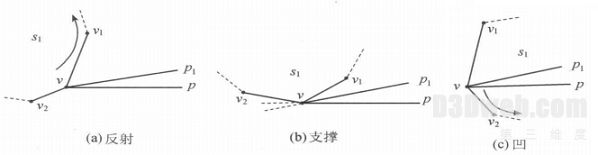
图 1 相对于线段 vp , vp1 点 v 的状态
Fig. 1 Status of point v relative to vp and vp1 lines

    新构造的三角网中, 每个三角形的点不可能来自同一凸壳, 因此存在 2 种可能的非法叠合情况, 如图 2 所示.

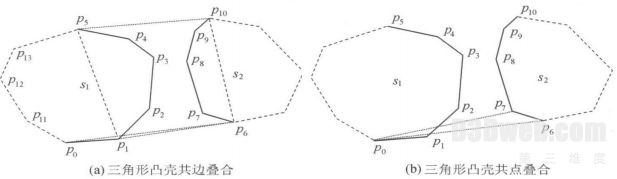
图 2 可能出现的 2 种叠合现象
Fig. 2 Two possible conquer instances

    为了避免缺陷三角形的出现, 需要对新构造的三角网进行判断. 构成新三角形的点一定来自于一个凸壳的相邻两顶点与另一凸壳上的单个顶点, 由此可得如下判定方法:

    a. 若单个顶点与有向线段共线或位于有向线段之左, p 0 相对于 p 6p 0 是凹的, 出现共边叠合现象, 如图 2(a) 中的 -p 0p 1p 6. 若某个凸壳上的相邻 2 点相对于另一凸壳上的单个顶点形成的线段是支撑或反射的, 则不会出现共边叠合, 如图 2( b) 中的 -p 7p 6p 0.

    b. 若相对于以单个顶点为端点、另一凸壳的相邻 2 点为另外两端点的两线段, 单个顶点是反射或支撑的, 就可避免出现共边叠合的现象. 图 1 所示为具体的判定方法: 若与单个顶点相邻的两顶点均在该顶点与另一凸壳的相邻 2 点形成的两条线段的一侧, 即顶点 v1, v 2 均在有向线段 vp, vp 1 的一侧, 则顶点 v 相对于vp, vp 1 是支撑的. 由于半凸壳点集是逆时针存储的, 若 v 沿顺时针方向的下一顶点v2 位于 vp , vp 1 之右, 且 v沿逆时针方向的下一顶点v1 位于 vp, vp 1 之左, 则 v 相对与vp, vp 1 是反射的. 在这 2 种情况下, 不会出现共边叠合现象.

    在竖直分割的条件下, 相当于顺时针旋转 90-, 其原理相同. 由此避免了寻找新点的繁琐步骤, 可得到新的子网合并算法.

    本文选取武汉市月湖清淤工程疏浚前的实测数据, 运用上述方法对月湖底泥地形进行仿真, 得到如图 3所示的三角网. 由图 3 可见, 使用分割合并算法很好地模拟了底泥地形, 但同时生成了很多并不属于月湖区域的冗余三角形, 因此需要剔除冗余三角形. 目前, 常用的剔除方法有 2 种: (a) 人工剔除; ( b) 设定阈值, 即在三角网生成完毕后, 判断每个三角形的边长, 若该三角形中有一条边的边长大于阈值, 则剔除该三角形. 第 1种方法的可操作性差, 当区域形状不规则、采样点多时, 费时费力. 第 2 种方法需要恰当的选取阈值, 难以把握.

图 3 月湖疏浚前 TIN 表示的底泥地形
Fig. 3 TIN of Yuehu Lake bottom before dredging

    2 包络三角网生成算法

    在生成三角网的过程中, 若能直接生成包围施工区的三角网, 则能避免冗余三角形的出现, 使重建的底泥地形更真实, 也方便TIN 数据的进一步处理. 一般的三角网生成算法在分割生成子域点集的凸三角网后,在合并的过程中会将 2 个子域凸三角网合并为 1 个新的凸三角网. 因此如果改变分割后合并的方法, 有可能生成符合区域原本形状的三角网. 若机械地分割施工区域, 将区域横向竖向分割为互相邻近的小矩阵, 在小矩阵内生成凸三角网再进行合并, 则可满足上述要求. 以图 4 为例, 其具体过程为: ( a) 找到包围采样点集的最小矩形, 遍历区域中的每个点, 找到最大、最小的 x, y 值, 形成该矩形的 4 个顶点坐标. ( b) 根据阈值分割矩形为 n - m 个小矩形, 寻找每个矩形内包含的点集, 使用逐点插入法建立小矩形的凸三角网. 若采样点过多, 则宜使用递归分割算法. ( c) 选择 x, y 方向上长度小的先进行子网合并. 如图 4 所示, 区域被分成 4 - 3 个小矩形, 生成小矩形的凸三角网后, 将纵向上的小凸多边形合并为4 个三角网, 再横向合并.

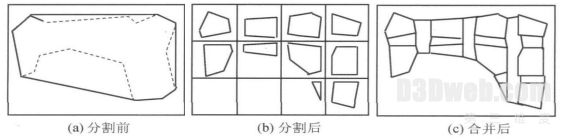
图 4 包络三角网生成算法示意图
Fig. 4 Generation algorithmfor enveloping triangulated network

    两凸多边形的合并过程为: 找到凸多边形的 x+ y, x- y的最大、最小值的 4 个点, 作为凸多边形合并的起始点与终止点, 这些点与夹在它们之间的凸多边形构成一个非凸多边形. 如图 5 所示, 对于生成的非凸多边形 C, 间隙三角网必在C 内构造. 构造的过程可表述为: 对于非凸多边形 C , 从其任一顶点 A 开始沿边界逆时针搜索; 若下一点为凸点, 则继续搜索; 若下一点为凹点, 即该点两邻边所夹内角大于 180-, 则继续搜索, 直至找到下一个凸点. 连接该凸点相邻的 2 个端点, 形成三角形, 并用构造的新边取代原来的两边. 不断循环直至所有的顶点均为凸点, 于是得到一个凸多边形与三角网, 将凸多边形分割为数个三角形之后即得到合并后的间隙三角网. 图 5( b) 所示三角网内的数字表示三角形的构造顺序, 首先生成三角形1, 依次分割得到三角形, 得到三角形 9 后, 余下一个凸多边形.

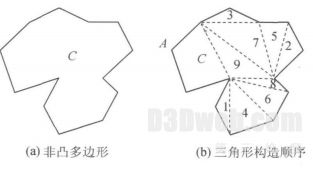
图 5 包络三角网的子网合并算法
Fig. 5 Subnetwork conquer algorithm forenveloping triangulated network

    选取凸多边形的 x+ y, x- y 的最大、最小值的 4 个点作为合并的起始点与终止点的依据是, 在凸多边形的边界上, 沿逆时针方向相邻顶点构成的邻边与水平或竖直方向的夹角大于 45-的所有点, 均认为是处于区域内部而非多边形边界上, 如图 6 所示. 根据地形边界条件的变化也可将该角度设为其他值, 也要相应地改变起始点与终止点的选取规则.

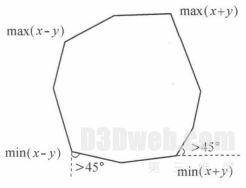
图6 起始点与终点的选取
Fig6 Selection of start and and points

    为方便算法实现, 将点集按逆时针存储为首尾相连的链表. 以竖直方向合并为例, 以下方的max( x- y)为起点、上方的 min(x - y) 为终点, 构成一个首尾相连的点链表, 然后循环判断链表中多边形顶点的凹凸特性. 判定方法是: 若目标顶点位于逆时针方向上的下一个相邻顶点与目标顶点构成的有向线段的右边, 则目标顶点为凹; 若在左侧, 则目标顶点为凸. 如图 7 所示, p 2 在有向线段 p 0p 1 的右侧, 则 p 1 为凹的, p 1 在有向线段 p 7p 0 的左侧, 则 p 1 为凸的.

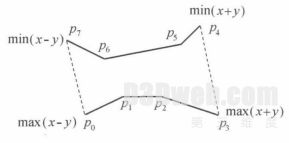
图7 顶点的存储规则
Fig.7 Storage of vertexes

    在生成三角形的过程中, 可能出现图8 所示的问题: (a)当需构造 AB 两凸域间隙非凸多边形时, 顺序连接顶点构造的间隙多边形可能非法. 如图8( a)所示, 顺序连接凸域 A 的 min(x - y )顶点 p 7 与凸域 B 中的max( x- y)顶点 p 0 构成的边 p 7p 0 时, 与 p 7 相邻的顶点 p 6 被置于多边形之外. ( b) 新构造的三角形将多边形的顶点包括在内, 如图 8( b)所示, p 4 为凹点, p 3 为凸点, 连接 p 4, p 0 形成的三角形将顶点 p 1 包括在内.

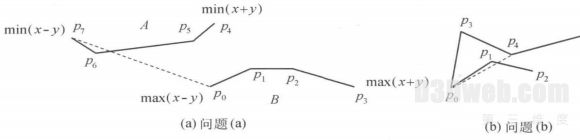
图 8 合并时可能出现的问题
Fig. 8 Possible problems during the conquer phase

    问题( a)的出现表明, 在构建图8 所示的间隙多边形之前, 需要对根据 x + y, x- y 值选择的始点与终点的合法性进行判断. 以 p 7 为例, 若 p 7 逆时针方向的下一个顶点 p 6 在有向线段 p 7p 0 的右侧, 则表明 p 7 非法,不能作为在凸域A 上进行合并的终点, 应将其删除, 然后将逆时针方向的下一个点 p 6 作为终点. 其他3 种情况原理相同.

    问题( b)的解决方法是: 在发现顶点 p 4, p 3, p 0 符合三角形生成原则时, 即 p 4 为凹点, p 3 为凸点后, 还应判断 p 0 的下一个顶点 p 1 是否在 -p 4p 3p 0 内, 如果不在, 则可连接 p 4p 0 生成三角形, 同时删除 p 3 点. 若在, 则应连接 p 1p 3 形成 -p 3p 0p 1, 同时删除 p 1 点.

    使用该方法选定月湖清淤工程疏浚前的实测数据, 将月湖区域分割为 40 - 10 个小矩形, 得到图 9 所示的三角网. 由不规则三角网生成算法的基本思想和实例结果可知, 该算法既结合了递归分割三角网合并算法的优势, 又能生成符合施工区域形状的包络三角网, 具体的效果取决于切割分辨率的选择以及采样点的分布, 算法要求采样点在边界上的分布必须完整.

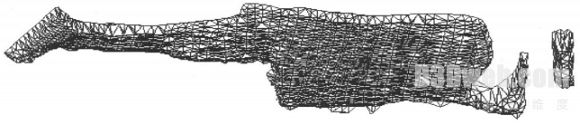
图 9 月湖疏浚前底泥的包络 TIN 网
Fig. 9 Enveloping TIN of Yuehu Lake bottom before dredging

    3 结 语

    运用三维地形仿真技术辅助环保疏浚工程施工, 已经被证明是十分有效的[10-11]. 本文重点研究了基于不规则三角网的地形建模算法, 改进了递归分割三角网合并算法, 提出了在进行子网合并过程中对生成的间隙三角网进行合法性判定的方法. 同时, 提出了一种包络三角网的生成算法, 能够直接生成与施工区域吻合的三角网, 避免了冗余三角形的出现. 分割分辨率的选取对算法效果影响较大, 当阈值过小时不能很好地吻合区域形状, 阈值过大时则建网时间过长. 在实际使用时应根据实际的地形形状, 选择合适的切割阈值.

    参考文献:

    [1] 刘文新, 栾兆坤, 汤鸿霄. 乐安江沉积物中金属污染的潜在生态风险评价[J]. 生态学报, 1999, 19( 2): 206-211.

    [2] 颜昌宙, 范成新, 杨建华. 湖泊底泥环保疏浚技术研究展望[J]. 环境污染与防治, 2004(6) : 189-191.

    [3] LEE D T, SCHACHTER B J.Two algorithms for constructing a Delaunay triangulation[J]. Int J of Computer and Information Sciences,1980, 9(3) : 72-74.

    [4] SLOAN S W. A fast algorithm for constructing delaunay triangulation in the plane[J] . Advanced Engineering Software, 1987, 9( 1): 34-55.

    [5] 刘学军, 龚健雅. 约束数据域的 Delaunay 三角剖分与修改算法[J] . 测绘学报, 2001, 30(1) : 82-88.

    [6] 陈鹰, 林怡. 基于数学形态学的 TIN 和GRID 自动生成研究[J] . 测绘学报, 2002, 31( 增刊) : 86-91.

    [7] 李志林, 朱庆. 数字高程模型[M] . 武汉: 武汉大学出版社, 2003: 78-91.

    [8] 武晓波, 王世新, 肖春生. 一种生成 Delaunay 三角网的合成算法[J]. 遥感学报, 2000, 4(1): 32-35.

    [9] 胡金星, 潘懋, 马照亭, 等. 高效构建 Delaunay 三角网数字地形模型算法研究[J] . 北京大学学报: 自然科学版, 2003(5) : 736-741.

    [10] BERG M DE, KREVELD M VAN. Computational geometry: algorithms and application[M] . Beijing:Tsinghua University Press, 2000: 207-233.

    [11] 康玲, 董纯. 基于 OpenGL Performer 的流域可视化仿真研究[J]. 华中科技大学学报: 自然科学版, 2003(6): 71-73.