来源：第三维度
    作者：孙 敏， 胡 争
    单位：北京大学遥感所
          中南大学信息物理工程学院

    摘要：近年来小型无人机在国际摄影测量领域的应用日益广泛，本文综述了目前国内外的相关发展现状，提出利用多视几何理论与技术，对国产微型无人机平台上获取的超低空影像进行计算处理的方法，实验结果表明，采用多视几何理论与技术可以很好的解决航空以及地面近景摄影测量的数据处理。

    1 引言

    近年来小型无人机（Mini-UAV, MUAV）在摄影测量领域的应用越来越受到人们的关注，国际上目前已有大量的相关研究，在这些研究工作中，通常采用各种辅助手段，如GPS 实时定位与INS 实时导航，可以使小型无人机的摄影测量相关精度达到毫米级。小型无人机摄影测量系统具有极为广泛的应用前景，其成果应用包括野外区域性勘测，如地质调查、水文调查、考古勘测、旅游规划、区域性测量（如大坝、桥梁）、环境监测（如洪水、泥石流），甚至化学事故与安全任务，乃至军事应用等等。小型无人机的最大优点是价格低、飞行基本不受空管限制、使用便捷、性能灵活稳定，可以在任何行业加以推广。无人机的种类很多，按Eisenbeiss划分(Eisenbeiss, 2004)，MUAV一般具有如下特点：飞行高度一般在1km以下；飞行半径约10km；起飞重量在30-150Kg 之间；续航时间约2 小时。而对于载荷在5kg 以下的无人机可称之为微型无人机。

    中型或微型无人机系统由于其平台的不稳定性以及其数据获取的特殊性，对后续数据处理提出了与传统数字化摄影测量有所不同的要求。数字化摄影测量近十多年来得到飞速发展，但其理论仍未得到实质性的突破，国内以张祖勋为代表的学者，提出了广义点摄影测量与多基线摄影测量（张祖勋2005, 2007），另外也有人提出了多视摄影测量的方法(崔红霞，2008)，但基础理论仍然是基于摄影测量中的共线方程。即意味着摄影测量数据获取过程必须满足两个条件之一：像对之间的相对旋转角应不大于6 度或相机摄影时的外方位元素初始值为已知。对于中型或大型飞机平台，或采用卫星定位系统（如GPS）与动态陀螺仪（INS）辅助作业的小型无人机平台，可以轻易地获取满足数据处理的相机外方位初始值，因此在实际生产中，摄影测量理论并没有遇到应用的障碍。

    但由于小型无人机系统特别是微型无人机系统在没有GPS 与INS 辅助作业的情况下，一般不易得到稳定的拍摄结果，影像之间偏转较大，难以采用传统的摄影测量数据处理方法进行后续数据处理。本文拟介绍一种采用多视几何理论与技术进行微型无人机后续数据处理的方法。

    2 研究现状

    MUAV 系统的研发历史可以回溯到上世纪七十年代由Dieter Schluter 研发的直升机模型，他的直升机模型在1980 年即由Wester-Ebbinghaus 用于摄影测量(Eisenbeiss, 2004)，当时的schluter 航模的有效载荷是3Kg。近年来，由于廉价且较高性能的GPS 与INS 系统的快速发展，使得MUAV近年在摄影测量领域受到国际上学者们与商家的广泛关注。

    国际上有许多著名的商家研制生产小型无人机，如Yamaha 公司生产的Yamaha-Rmax具有双引擎，可续航21小时，最大起飞重量为95Kg；Schiebel公司生产的Camcopter S-100型无人机最大有效载荷为50Kg，最大续航6 小时(http://www.schiebel.net/)。另外国际上有许多公司和机构在研发小型无人机系统，如荷兰Geocopter 公司（http://geocopter.nl）；瑞士苏黎世Aeroscout GmbH 公司（http://www.aeroscout.ch/company.html）等等。

    国内近年来对小型无人机摄影测量系统的发展非常重视，如汶川地震后，中兵光电科技公司研制的型号为“华鹰”的无人机迅速得到了应用，并取得了出色的航拍成绩。该无人机起飞重量20Kg，翼展2.6m，续航时间约3 小时，属于微型无人机，装备有号称国内最先进的无人机遥感测绘系统，采用GPS自主导航，数据链传输可达30公里，价值约120 万。但该无人机后续数据处理方法与结果并未公开。总体上，中国在该方面的研究明显落后于国际先进水平（如图1 所示为一些典型的商业无人机系统）。

图 1. 几种著名的小型无人机从左到右依次为Schebel、Yamaha Rmax、Helicam以及国产华鹰品牌

    2004 年在伊斯坦布尔召开的国际摄影测量大会上，有三篇论文阐述了UAV摄影系统，其中包括中国测绘科学院的无人机系统（Nagai 2004，Schwarz 2004，Wang 2004）。而2008年7 月初在北京召开的ISPRS大会上，专门设立了一个名为UAV for Mapping的专题，据作者不完全统计至少有十多篇论文阐述了UAV 摄影测量系统。绝大多UAV 数摄影测量系统具有较大的载荷，可以同时搭载数码相机与激光扫描系统，并配备GPS 与INS 系统，因此可以较好地完成测量任务。其中典型的工作有：来自日本的Nagai 介绍了一种使用IMU 与GPS 组合导航，将数码相机与激光扫描仪一起搭载进行三维成图的摄影测量系统；来自瑞士的Eugster 介绍了一种小型无人机摄影测量系统，将其用于影像及地理信息的实时获取；来自德国的Grenzdörffer 介绍了一种微型无人机系统，其载荷不大于5kg，比小型无人机具有更低的成本和更高的灵活性。另外，国内林宗坚介绍了一种飞艇摄影测量系统。

    总体而言，为了获取良好的测绘成果，绝大多数MUAV系统采用了GPS与INS组合的导航方式，从而使得采用传统数字摄影测量的方法进行后续处理完全可行。但对于无GPS与INS 辅助的系统或微型无人机系统，必须考虑采用新的数据处理方法。下面作者介绍采用多视几何理论的无人机数据处理方法。

    3 多视几何理论

    多视几何（Multiple view geometry）理论在计算机科学领域近十多年来得到了长足的发展，国际上已有一些经典性的文献（如: Hartley 2002, Ma 2003）。同时，也有许多学者就多视几何理论引入到摄影测量领域的工作进行了深入研究，但目前仍没有相对成熟的工作。

    多视几何理论与传统摄影测量理论有一定的差异，同时各有优缺点（孙敏2007）。当像对间的旋转角较大时，选择多视几何理论进行计算处理是一种经济便捷的方法。

    3.1 基本矩阵

    多视几何理论进行摄影测量数据处理的前提条件只需要像对有足够的重叠度，而对相机外方位元素无任何要求。像对的重叠度越大，得到的结果越可靠，即精度越高。假设一像对由A、B 两影像组成，则A 与B 上点和线的空间关系即可由基本矩阵或本质矩阵表达。基本矩阵的定义如下：

    设 x 与x'分别为A与B上的对应像点，则基本矩阵F满足条件式：x'TFx = 0。F的几何意义是，点x 在B上的对应点x'必然在过B核点的直线上。F是一个3x3 的矩阵，其秩为2，因此其计算只需要7 个同名像点对即可。由于F 一般是一个奇异矩阵，因此通常须采用奇异值分解法得到稳健的结果。

    3.2 投影矩阵与三维点集计算

    投影矩阵的实质是摄影测量中的共线条件方程。在摄影测量中一般由一些初始值直接计算。但在多视几何理论中，投影矩阵由基本矩阵分解得到。设两影像A与B的投影矩阵分别为P1与P2，则其与基本矩阵F有如下关系（Hartley2002）：

    设基本矩阵为F，影像B的核点为e'，且存在一个偏斜矩阵S，则P1与P2可表达为：

    P1 = [I | 0] P2 = [SF | e']

    通常 S可选择e'构成的斜对称矩阵，即可令S = [e']x。

    令与同名像点x 与x'对应的三维点为X，则：x = P1X, x' = P2X。故当P1与P2均已知时，即可求得三维点X。

    3.3 深度图与表面模型生成

    通常由于通过自动提取与匹配的同名像点数量较少且分布不均，因此必须进行深度图计算以得到精确表达对象（如地面或目标表面）的点云。传统摄影测量中，一般采用沿核线匹配的方法得到地形表面模型。在多视几何中，通常先将影像为其 影像， 影像上的行扫描线即为核线，从而使深度图计算过程中的匹配限制在对应行扫描线上，以加快匹配处理。

    假设影像A与B的影像分别为A'与B'，则A' = H1A，B' = H2B。H 矩阵为对应矩阵，在投影中不存在平的情况下，H 矩阵了两平面间的对应点投影关系，H 的计算可以考文献（Koch, 1995）。

    后的影像通过沿行扫描线进行匹配的方法得到对应点的视差也即深度。影像上所有像点的视差即构成了像对的深度图。当深度图已知时，对于续表面如地形表面而言，即可通过三角会的方法得到实的三维点云，对三维点云进一处理，即可得到对象的三维表面模型。

    4 影像数据处理方法及实验系统

    在本项研究中， 们采用北京东方航空公司研制的AF2000 微型无人机所获取的影像（ 后文图4）。该无人机最大载荷为5kg，起飞重量为20kg，翼展2.5m，最大航高1km，续航能可达 4-5 小时。如图2 为AF2000 微型无人机。具体们采用了如下数据处理方法：

图2. AF2000微型无人机

    ☆ 分别对影像进行特点提取，通常采用Harris算法即可得到较理的特点，但对不同的影像内也可以选择其算法；

    ☆ 进行影像特点匹配，匹配的大小以及将直接影匹配的结果，一般可按图像的大小决定；由于匹配一般不可，因此通常采用RANSAC算法，具体可考文献（Hartley 2002）；

    ☆ 由于匹配过程中同时计算基本矩阵是一种稳健的方法，因此特点匹配与基本矩阵计算通常环进行；

    ☆ 投影矩阵可按3 所述内 由基本矩阵分解得到。

    ☆ 利用对应像点，结合投影矩阵，即可得到三维点。

    ☆ 利用投影矩阵计算得到对应矩阵， 利用对应矩阵进行影像，得影像。

    ☆ 对两影像沿行扫描线进行匹配，计算得到视差深度图。依据深度图即可求得对象的三维表面模型。

    为了获取稳健的结果，一般在拍摄前需要对相机进行，如有必要，在拍摄后也应对相机一次。如图3 为们基于多视几何理论开发的摄影测量数据处理实验系统。

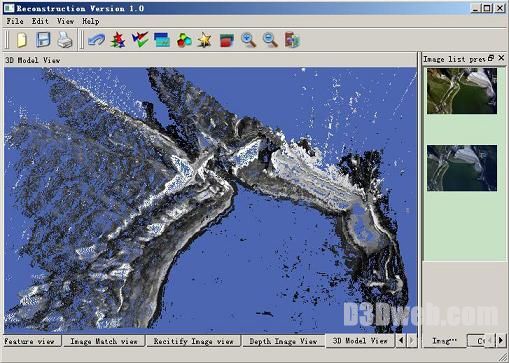
图3. 基于多视几何理论开发的摄影测量数据处理实验系统

a)

b)

c)

d)
图4. a 和b为本文实验采用的AF2000无人机获取的立体像对，
c为匹配的结果，d为深度图

    图4 为实验所用像对与各主要的所得结果。图3中面图中所示为该像对最计算所得三维点云。由于采用多视几何理论进行数据处理时，对相机外方位元素无要求，因此本实验所开发的系统不可用于航空摄影情形，同时也可以很好地用于地面近景摄影测量，如图5为们为我们采用通数码相机拍摄的北大红一公 的影像对，通过一系处理得到了较好的结果。

    5 结论

    以上研究表明，基于多视几何理论的摄影测量数据后处理方法完全是可行而且有效的，但目前仍然是一个值得深入研究的方， 其是其应用将着小型与微型无人机系统的推广而应有极大的发展。本文作为一项性的研究，有许多题仍有进一解决。如，图像内差万别，同时由于一些典型区域，如水域、面等的存在，因而深度图生成过程中，不可将产生一些匹配，如何在自动化过程中生成完的深图仍将是本项研究进一需要的工作。同时长影像的快速处理也是一项有深入研究的题。另外，由于在本项研究中没有考虑制点的题， 然可以对三维重构结果的精度进行一定的计，由于多视几何采用了非线性方程进行数据计算，故目前仍缺的精度方法。

    参考文献

    [1]. 张祖勋， 生 等. 多基线-数字近景摄影测量[J]. 地理空间信息，Vol.5, No.1, 2007.2, p1-4.

    [2]. 张祖勋，张. 广义点摄影测量及其应用. 大学学信息科学，Vol. 30. No.1, 2005, p1-5

    [3]. 崔红霞，林宗坚等. 无人飞艇低空数码影像多视摄影测量[J]. 光电工程，Vol.35, No.7，2008.7，p73-78.
   
    [4]. Eisenbeiss H., 2004. AMini Unmaned Aerial Vehicle: System Overview and Image Acquisition,http://www.photogrammetry.ethz.ch/pitsanulok_workshop.

    [5]. Nagai, M., Shibasaki, R., et al., 2004. Development of digital Surface and feature extraction by integratinglaser scanner and CCD sensor with IMU, ISPRS2004, Istanbul,Vol. XXXV, Part B5.

    [6]. Wang JZ, Lin ZJ, et al, 2004. Reconstruction of buildings from a single UAV image. ISPRS2004, Istanbul,Vol. XXXV, Part B8.

    [7]. Schwarz, K., P., El-Sheimy, N., 2004. Mobile Mapping Systems – State of the art and future trends.ISPRS2004, Istanbul, Vol. XXXV, Part B1.

    [8]. LIN Z.J., 2008. UAV for Mapping—Low Altitude Photogrammetric Survey, ISPRS2008, Beijing, 2008, Vol.XXXVII, p1183-1187.

    [9]. Nagai M., Chen T.N., et al, 2008. UAV Borne Mapping by Multi Sensor Integration, ISPRS2008, Beijing,2008, Vol. XXXVII, p1215-1223.

    [10]. Eugster H., Nebiker S., 2008. UAV-Based Augmented Monitoring – Real-Time Georeferencing andIntegration of Video Imagery with Virtual Globes, ISPRS2008, Beijing, 2008, Vol. XXXVII, p1229-1237.

    [11]. Grenzdörffer G. J., Engel A., Teichert B., 2008. The Photogrammetric Potential of Low-Cost UAVS inForestry and Agriculture, ISPRS2008, Beijing, Vol. XXXVII, p1207-1215.

    [12]. Hartley R., Zisserman A., 2002. Multiple View Geometry in Computer Vision[M], Cambridge UniversityPress, 2002.

    [13]. Ma Y., Soatto S., et al, 2003. An Invitation to 3-D Vision: From Images to Geometric Models,Interdisciplinary Applied Mathematics, Springer, November 2003.

    [14]. 孙敏. 多视几何与传统摄影测量理论. 北京大学学自然，2007, Vol.43, No.4, p453-460.

    [15]. Koch R., Surface Reconstruction from Stereoscopic Image Sequences, ICCV95, 1995, p109-113.

    作者简介

    孙敏：1968 年生，2000 年获士学位，现为北京大学遥感所，主要研究方为： 现实地理信息系统和基于影像的三维重构。地址 ：北京和 5 号，北京大学遥感所，100871  电话：010-62764484 Email: sunmin@pku.edu.cn ：http://www.argis.cn

    胡争：1984 年生，中南大学信息物理工程学院研究生/北京大学遥感所研究生，主要研究方为：基于影像的三维重构。地址 ：北京和 5 号，北京大学遥感所，100871 电话：010-62764484 Email: huzheng_csu@163.com