式中：n为金字塔图层序号(从第0层起算)；rowID与columnID分别为地图瓦片在金字塔在第n层中的行号与列号；TotalRow与TotalColumn为金字塔第0层瓦片的总行数与总列数，为常数。

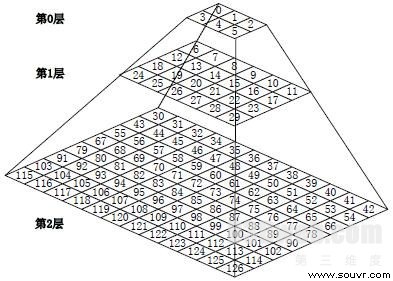
图1 不规则地图金字塔的分层与编码

    如果该地图瓦片为三维仿真地图类型，那么该瓦片编码将会有一个后缀，后缀代表该三维仿真地图瓦片的视角代码，每个视角的地图对一个地图视角代码。金字塔群组中所有的地图瓦片按照编码顺序存储在数据库中，每一个地图编码对应金字塔群组中唯一的地图瓦片。如“3D-126-1”表示在视角代码为“1”的三维仿真地图子金字塔中，编码为“126”的地图瓦片。

    3 三维仿真地图的坐标转换

    3.1 坐标系统介绍

    多视角三维仿真城市采用的二维地图数据与遥感影像数据都是经过数据校正处理的，其像素坐标系统与地理坐标系统是直接匹配的，是已经建立了地理参考的。

    三维仿真地图在本质上是栅格地图，对于每个视角的三维仿真地图，赋予一套统一的逻辑坐标系统，使不同图层的仿真地图处于同一套逻辑坐标下，但不同视角的三维仿真地图采用不同的逻辑坐标系统，它们之间是相互独立的。逻辑坐标采用三维仿真地图底层图层的像素坐标，即三维仿真地图的逻辑坐标系统与地图底层图层的像素坐标是等价的，显然，该逻辑坐标是不同地图层的像素坐标的2的整数次幂的倍数。

    三维仿真地图的逻辑坐标系统是相对独立的，没有匹配到地理坐标系上，因此三维仿真地图的逻辑坐标没有地理参考意义，无法直接在三维仿真地图上直接实现计算方向、面积、距离等地理功能。

    三维仿真地图采用倾斜视角，增强了三维仿真地图的视觉立体感，同时也造成了三维仿真地图的地理形变，但通过简单的几何纠正把三维仿真地图匹配到地理坐标系上，将严重影像三维仿真地图的三维视觉效果。这里可以建立三维仿真地图逻辑坐标与地理坐标的转换关系，在需要显示特定地理坐标位置的三维仿真地图数据时，将地理坐标转换为三维仿真地图的逻辑坐标，满足地图的显示。而在需要进行地理计算的时候才将三维仿真地图的逻辑坐标转换为地理坐标，来进行地理计算实现地理功能。

    这样既保留了三维仿真地图的良好的视觉效果，又保证了三维仿真地图的精确的地理计算功能。

    3.2 坐标转换原理

    三维仿真地图逻辑坐标系统到地理坐标系统的转换，可以借助同一区域经过地理校正的二维地图数据作为参考，建立三维仿真地图逻辑坐标空间与二维地图地理坐标空间的转换关系。

    虽然三维仿真地图与二维地图对现实世界采用了不同的表现形式，但展示是同一区域的地理信息。三维仿真地图空间可以认为二维地图空间在经过了旋转、平移、缩放、扭曲等一系列几何变换之后得到，的这个几何变换的过程可以建立数学模型进行模拟，根据二维地图与三维仿真地图的同名控制点的坐标数据来拟合多项式方程，从而得到三维仿真地图逻辑坐标到二维地图的地理坐标的转换关系，二维地图地理坐标到三维仿真地图的坐标转换可以认为是上述几何变换的逆过程。

    3.3 坐标转换的实现方法

    令三维仿真地图空间与二维地图地理空间分别为F(x,y)与G(μ,ν)，L为两平面之间的坐标转换关系，则两个平面之间的坐标转换方程可以描述为：

    坐标转换要解决的是对转换函数L的求解问题，由于两地图空间的几何变换参数并不明确，这里可以采用多项式来模拟转换函数L ，求解转换参数，于是有：

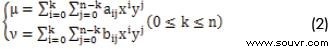
    两地图空间之间的坐标转换问题， 就转变成了对上述方程系数a i j ,bi j的求解问题。式中n为多项式的次数, 多项式的项数以及系数的个数为(n(n+3)/2+1)，相应的至少需要(n(n+3)/2+1)组控制点数据来计算多项式的参数，如果有多余的观测数据,这里采用满足最小二乘的条件来求解,即满足：

    式中为真值， 为计算值。按照求极值原理有：

    将(3)带入(4)整理后可得：

    式(5)中：

    这样就完成了对坐标转换的函数L的求解，得到了坐标转换参数，该坐标转换公式的误差估计和精度可分别由(6)、(7)式算得，来进一步评定获得的转换参数是否满足精度要求。

    误差公式为：